Article

Instrument Pricing Analytics - Zero-Coupon Curves

May 24,2021

Umer Nalla

In one of my earlier articles on Instrument Pricing Analytics - Volatility Surfaces and Curves, I promised I would deliver a follow-up article on Zero Coupon Curves - another of related the IPA content sets.

Zero-Coupon Curves, like other pricing data (Volatility Surfaces, Inflation Curves), are used to model risk factors and can be used to power risk management or valuation systems.

As with the previous article, I think the best way to highlight this content is via some code and a few graphs - so let me dive straight into the code....

Initialisation

The first thing I need to do is import my libraries and then run my scripts to define my helper functions. As you will note I am importing the Refinitiv Data Platform library which will be my main interface to the Platform - as well as few commonly used Python libraries.

    	
            import json

import refinitiv.dataplatform as rdp

import configparser as cp

from IPython.display import HTML

import matplotlib.pyplot as plt

import pandas as pd



%run "../plotting_helper.ipynb"

As the name would suggest, the plotting_helper contains the full plotting code. I won't share any of the plotting code snippets in this article - please refer to the actual file on GitHub (see link in right hand panel).

Connect to the Refinitiv Data Platform

I fetch my credentials from a configuration file and use them to open a Platform session - If I were a Desktop user of Eikon or Refinitiv Workspace, I could open a Desktop session instead.

    	
            config = cp.ConfigParser()

config.read("c:/Refinitiv/config.cfg")

session = rdp.open_platform_session(config['platform']['app_key'],

    rdp.GrantPassword( username=config['platform']['user'],

    password=config['platform']['password'] )

)

Endpoint Interface

In my previous article I mentioned how the Refinitiv Data Platform library consists of different layers:

Function: Highest level - single function call to get data
Content: High level - Fuller response and Level 1 Streaming data too
Delivery: For Level 2 Streaming data and data sets not supported by above Layers

Whilst there is some support for IPA data in the Function Layer, I will use the Delivery layer as it works for all IPA content on the platform. Each unique content set on the Platform has its own Endpoint and we can use the Delivery Layers Endpoint interface to access that content.

Using the Endpoint interface to request IPA content is fairly straightforward

Identify the required IPA Endpoint (URL)
Use the Endpoint Interface to send a request to the Endpoint
Decode the response and extract the IPA data

Identifying the Surfaces Endpoint

To ascertain the Endpoint, we can use the Refinitiv Data Platform's API Playground - an interactive documentation site you can access once you have a valid Refinitiv Data Platform account.

So, firstly I can search for 'curves' to narrow down the list of Endpoints and then select the relevant Endpoint from the list. At the time of writing, their 3 related Endpoints available and I will use all of them in this article.

I copy the required Endpoint URLs e.g. - /data/quantitative-analytics-curves-and-surfaces/v1/curves/zc-curves - to use with the Endpoint interface as follows:

Define our API Endpoints for the ZC Curve definitions and ZC Curves data

    	
            zcCurveDefinitions_endpoint = rdp.Endpoint(session,

    'https://api.refinitiv.com/data/quantitative-analytics-curves-and-surfaces/v1/curves/zc-curve-definitions')



zcCurve_endpoint = rdp.Endpoint(session,

    'https://api.refinitiv.com/data/quantitative-analytics-curves-and-surfaces/v1/curves/zc-curves')



forward_zcCurve_endpoint = rdp.Endpoint(session,

    "https://api.refinitiv.com/data/quantitative-analytics-curves-and-surfaces/v1/curves/forward-curves")

Querying Curve Definitions

Before we can request a ZC Curve we need to have an idea of what curves are actually available on the Refinitiv Data Platform.

Our interactions with the platform take the form of JSON messages i.e. JSON requests and JSON responses.

We can use the Curve Definitions Endpoint to discover what is currently available by sending a JSON request.

For instance, if I want to discover the full list of what Refinitiv has available in terms of ZC Curves, I can send a request with a single parameter i.e. the Source:

    	
            request_body={
  "universe": [
    {
      "source": "Refinitiv"
    }
  ]
}
 
response = zcCurveDefinitions_endpoint.send_request(
    method = rdp.Endpoint.RequestMethod.POST,
    body_parameters = request_body
)
 
pd.DataFrame(data=response.data.raw["data"][0]["curveDefinitions"]).sort_values(by='currency')

currency	mainConstituentAssetClass	riskType	indexName	source	name	firstHistoricalAvailabilityDate	id	availableTenors	availableDiscountingTenors	marketDataLocation
AED	Swap	InterestRate	AEIBOR	Refinitiv	AED AEIBOR Swap ZC Curve	2016-12-07	95da64b1-e96f-4d60-8df1-63d8484017d6	[6M, 1Y, 3M]	[6M, 1Y, 3M]	NaN
AUD	Swap	InterestRate	BBSW	Refinitiv	AUD BBSW Swap ZC Curve	2016-11-07	a69788a8-114a-476a-998e-48404dab43ee	[6M, OIS, 3M, 1M]	[6M, OIS, 3M, 1M]	NaN
BHD	Swap	InterestRate	BHIBOR	Refinitiv	BHD BHIBOR Swap ZC Curve	2016-02-08	6463b459-8c98-40a5-a779-a58967f22435	[3M]	[3M]	NaN
BRL	Swap	InterestRate	DICLOSE	Refinitiv	BRL DI Swap ZC Curve	2011-01-05	0aa32067-d7d9-48f0-908b-4a12281207f8	[1D]	[1D]	NaN
CAD	Swap	InterestRate	CORRA	Refinitiv	CAD CORRA Swap ZC Curve	2015-04-22	447736a8-743d-413d-8640-953470baaf23	[OIS]	[OIS]	NaN
...	...	...	...	...	...	...	...	...	...	...
USD	Swap	InterestRate	SOFR	Refinitiv	USD SOFR Swap ZC Curve	2020-06-17	34d8c1f9-8fd1-4ca3-bb37-5464c41de2f7	[OIS, 3M]	[OIS]	NaN
USD	Swap	InterestRate	LIBOR	Refinitiv	USD LIBOR Swap ZC Curve	2014-09-25	1ef0692f-1cde-4b71-bad7-e39198633e0e	[6M, OIS, 3M, 1M]	[6M, OIS, 3M, 1M]	NaN
USD	Futures	InterestRate	LIBOR	Refinitiv	USD EURODOLLAR Futures Curve	2014-09-25	0e304ce8-dcbf-44cd-a1fe-d36c1b4eb3a6	[3M]	[3M]	NaN
VND	Swap	InterestRate	VNDVNIBOR	Refinitiv	VND VNDVNIBOR Swap ZC Curve	2006-02-10	34505484-6279-430e-a219-62aa97e03b15	[3M]	[3M]	NaN
ZAR	Swap	InterestRate	JIBAR	Refinitiv	ZAR JIBAR Swap ZC Curve	2007-07-09	cddabbc7-5e83-4c01-93d7-51da53ee6f64	[3M]	[3M]	NaN

I extract the Curve Definitions data from the JSON response and convert it to a Pandas Dataframe for easier viewing.
As you will note, the definition includes various properties including the Currency as well as available Tenors and Discounting Tenors.

At the time of writing, we had 61 Curves available from Refinitiv on the Data Platform.
It is possible that in the future we could offer Curves from other non-Refinitiv Sources.

Filtering the list of Curve Definitions

You can restrict the list of curves returned by specifying a filter e.g. Currency:

    	
            request_body={
  "universe": [
    {
      "source": "Refinitiv",
      "currency": "USD"
    }
  ]
}
 
response = zcCurveDefinitions_endpoint.send_request(
    method = rdp.Endpoint.RequestMethod.POST,
    body_parameters = request_body
)
 
df = pd.DataFrame(data=response.data.raw["data"][0]["curveDefinitions"])

currency	mainConstituentAssetClass	riskType	indexName	source	name	firstHistoricalAvailabilityDate	id	availableTenors	availableDiscountingTenors
USD	Swap	InterestRate	LIBOR	Refinitiv	USD LIBOR Swap ZC Curve	2014-09-25	1ef0692f-1cde-4b71-bad7-e39198633e0e	[6M, OIS, 3M, 1M]	[6M, OIS, 3M, 1M]
USD	Futures	InterestRate	LIBOR	Refinitiv	USD EURODOLLAR Futures Curve	2014-09-25	0e304ce8-dcbf-44cd-a1fe-d36c1b4eb3a6	[3M]	[3M]
USD	Swap	InterestRate	SOFR	Refinitiv	USD SOFR Swap ZC Curve	2020-06-17	34d8c1f9-8fd1-4ca3-bb37-5464c41de2f7	[OIS, 3M]	[OIS]

Note how we have 3 curves for USD - this applies to many other currencies also, e.g EUR, JPY and so on.
You can refer to the curve properties to identify the differences e.g. a given currency may have curves based on different indices as well as Market Data Locations e.g. if I repeat the above request for JPY, you will note the MarketDataLocation column:

currency	mainConstituentAssetClass	riskType	indexName	source	name	marketDataLocation	firstHistoricalAvailabilityDate	id	availableTenors	availableDiscountingTenors
JPY	Swap	InterestRate	TIBOR	Refinitiv	JPY TIBOR (EMEA) Swap ZC Curve	EMEA	2015-08-13	a865716b-e437-4045-84b5-f6483d8b6a25	[6M, OIS, 3M, 1M]	[6M, OIS, 3M, 1M]
JPY	Swap	InterestRate	TONAR	Refinitiv	JPY TONAR Swap ZC Curve	NaN	2014-06-23	ac40f851-2333-4f2e-ade2-8928bc0e2072	[OIS]	[OIS]
JPY	Swap	InterestRate	LIBOR	Refinitiv	JPY LIBOR Swap ZC Curve	NaN	2010-06-23	cbf84acf-5328-4efc-8d23-f476ac495d82	[6M, OIS, 3M, 1M]	[6M, OIS, 3M, 1M]
JPY	Swap	InterestRate	TIBOR	Refinitiv	JPY TIBOR Swap ZC Curve	NaN	2015-08-13	e24f1a57-9007-4535-a4d7-b037662ace95	[6M, OIS, 3M, 1M]	[6M, OIS, 3M, 1M]

Requesting a curve by its ID

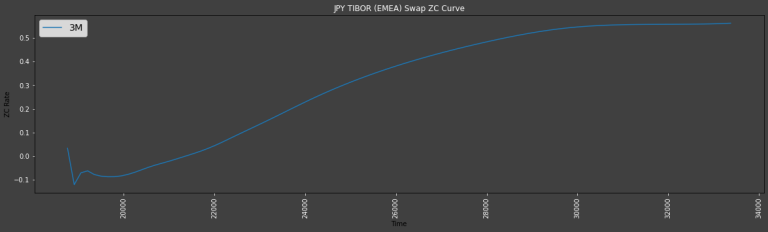
Once you have discovered the ID of a curve you can request it directly - for example, the JPY TIBOR (EMEA) Swap ZC Curve - note that I have selected the 1M Discounting Tenor from the available ones:

    	
            request_body = {
    "universe": [
        {
            "curveDefinition": {
                "id": "a865716b-e437-4045-84b5-f6483d8b6a25",
                "discountingTenor": "1M"
            }
        }]
}
 
response = zcCurve_endpoint.send_request(
    method = rdp.Endpoint.RequestMethod.POST,
    body_parameters = request_body
)

Detailed Response - curve points data - Definition + Parameters

Note how the JSON Responses Curve points data is preceded by the full definition and the default Parameters that were used to generate the curve.
One use for this would be, for example, If you wanted to request a user-defined curve (see later) with some variations, you could extract these details from the response and tweak some of the parameters to form your own custom request.

    	
            print(json.dumps(response.data.raw, indent=2))
{
  "data": [
    {
      "curveParameters": {
        "extrapolationMode": "None",
        "interpolationMode": "CubicDiscount",
        "interestCalculationMethod": "Dcb_Actual_Actual",
        "priceSide": "Mid",
        "calendarAdjustment": "Calendar",
        "calendars": [
          "JAP_FI"
        ],
        "compoundingType": "Compounded",
        "useMultiDimensionalSolver": true,
        "useConvexityAdjustment": true,
        "useSteps": false,
        "convexityAdjustment": {
          "meanReversionPercent": -6.9637,
          "volatilityPercent": 0.142
        },
        "valuationDate": "2021-05-17",
        "ignoreExistingDefinition": false
      },
      "curveDefinition": {
        "availableTenors": [
          "OIS",
          "1M",
          "3M",
          "6M"
        ],
        "currency": "JPY",
        "mainConstituentAssetClass": "Swap",
        "riskType": "InterestRate",
        "indexName": "TIBOR",
        "source": "Refinitiv",
        "name": "JPY TIBOR (EMEA) Swap ZC Curve",
        "marketDataLocation": "EMEA",
        "id": "a865716b-e437-4045-84b5-f6483d8b6a25",
        "discountingTenor": "1M",
        "indexTenors": [
          "1M",
          "3M",
          "6M"
        ]
      },
      "curves": {
        "1M": {
          "curvePoints": [
            {
              "discountFactor": 1.0,
              "endDate": "2021-05-17",
              "ratePercent": 0.033463900578256656,
              "startDate": "2021-05-17",
              "tenor": "0D"
            },
            {
              "discountFactor": 0.9999981666700277,
              "endDate": "2021-05-19",
              "ratePercent": 0.033463900578256656,
              "startDate": "2021-05-17",
              "tenor": "2D"
            },
            {
              "discountFactor": 0.9999917500562983,
              "endDate": "2021-05-26",
              "ratePercent": 0.03346384092193233,
              "startDate": "2021-05-17",
              "tenor": "1W",
              "instruments": [
                {
                  "instrumentCode": "ZTIJPY1WD="
                }
              ]
            },
            {
              "discountFactor": 0.9998634350721518,
              "endDate": "2021-06-21",
              "ratePercent": 0.14252891203141438,
              "startDate": "2021-05-17",
              "tenor": "1M",
              "instruments": [
                {
                  "instrumentCode": "ZTIJPY1MD="
                }
              ]
            },
...

Truncated

...
        ],
          "isDiscountCurve": false
        }
      }
    }
  ]
}

Plot the data

I can then use the curve points to generate my curve plot:

OR if I wanted to get the data into a Pandas Dataframe for some number crunching:

    	
            pd.DataFrame(response.data.raw['data'][0]["curves"]["3M"]["curvePoints"])

discountFactor	endDate	ratePercent	startDate	tenor	instruments
1.000000	2021-05-17	0.033464	2021-05-17	0D	NaN
0.999998	2021-05-19	0.033464	2021-05-17	2D	NaN
0.999992	2021-05-26	0.033464	2021-05-17	1W	[{'instrumentCode': 'ZTIJPY1WD='}]
0.999863	2021-06-21	0.142529	2021-05-17	1M	[{'instrumentCode': 'ZTIJPY1MD='}]
1.000164	2021-08-19	-0.063774	2021-05-17	3M	[{'instrumentCode': 'ZTIJPY3MD='}]
1.000337	2021-11-19	-0.066050	2021-05-17	6M	[{'instrumentCode': 'JPAM3T6M=TRDT'}]
1.000519	2022-02-21	-0.067671	2021-05-17	9M	[{'instrumentCode': 'JPAM3T9M=TRDT'}]
1.000645	2022-05-19	-0.064066	2021-05-17	1Y	[{'instrumentCode': 'JPAM3T1Y=TRDT'}]
1.001128	2022-11-21	-0.074359	2021-05-17	1Y6M	[{'instrumentCode': 'JPAM3T18M=TRDT'}]
1.001698	2023-05-19	-0.084557	2021-05-17	2Y	[{'instrumentCode': 'JPAM3T2Y=TRDT'}]
1.002592	2024-05-20	-0.086010	2021-05-17	3Y	[{'instrumentCode': 'JPAM3T3Y=TRDT'}]
1.002792	2025-05-19	-0.069584	2021-05-17	4Y	[{'instrumentCode': 'JPAM3T4Y=TRDT'}]
1.002218	2026-05-19	-0.044252	2021-05-17	5Y	[{'instrumentCode': 'JPAM3T5Y=TRDT'}]
1.001440	2027-05-19	-0.023959	2021-05-17	6Y	[{'instrumentCode': 'JPAM3T6Y=TRDT'}]
1.000166	2028-05-19	-0.002364	2021-05-17	7Y	[{'instrumentCode': 'JPAM3T7Y=TRDT'}]
0.998355	2029-05-21	0.020550	2021-05-17	8Y	[{'instrumentCode': 'JPAM3T8Y=TRDT'}]
0.995631	2030-05-20	0.048617	2021-05-17	9Y	[{'instrumentCode': 'JPAM3T9Y=TRDT'}]
0.991845	2031-05-19	0.081874	2021-05-17	10Y	[{'instrumentCode': 'JPAM3T10Y=TRDT'}]
0.987403	2032-05-19	0.115251	2021-05-17	11Y	[{'instrumentCode': 'JPAM3T11Y=TRDT'}]
0.982318	2033-05-19	0.148712	2021-05-17	12Y	[{'instrumentCode': 'JPAM3T12Y=TRDT'}]
0.963050	2036-05-19	0.251225	2021-05-17	15Y	[{'instrumentCode': 'JPAM3T15Y=TRDT'}]
0.925878	2041-05-20	0.385647	2021-05-17	20Y	[{'instrumentCode': 'JPAM3T20Y=TRDT'}]
0.887247	2046-05-21	0.479464	2021-05-17	25Y	[{'instrumentCode': 'JPAM3T25Y=TRDT'}]
0.850356	2051-05-19	0.541698	2021-05-17	30Y	[{'instrumentCode': 'JPAM3T30Y=TRDT'}]
0.823069	2056-05-19	0.557791	2021-05-17	35Y	[{'instrumentCode': 'JPAM3T35Y=TRDT'}]
0.798879	2061-05-19	0.562865	2021-05-17	40Y	[{'instrumentCode': 'JPAM3T40Y=TRDT'}]

Note the final column, which shows the Instrument that was used for the bootstrapping when generating the individual curve points

Requesting Curve using Parameters

As an alternative to using the Curve ID, I can also request a curve using Curve Parameters and Definition values.
Some of the key Parameters here are:

Valuation Date
InterpolationMode e.g. CubicSpline, CubicDiscount, Linear etc
Day Count Basis e.g.
- Actual, AFD, ISDA, 360, 365...
- 30_360, 30_360_US, 30_360_German...
- 30_365, 30_365_US, 30_365_German...

One thing to be aware of here is that if we had more than one EUR curve, I would need to specify sufficient Definition parameters to uniquely identify the curve I want.
So, for example if we had two 'EURIBOR' based curves, I would need to specify the full name as well (or other unique definition parameter) - but as we currently only have one I can just specify the indexName as I have done below.

    	
            request_body={
    "universe": [
    {
        "curveParameters": {
            "valuationDate":"2020-06-30",
            "interpolationMode": "CubicSpline",
            "priceSide": "Mid",
            "interestCalculationMethod": "Dcb_Actual_Actual",
            "extrapolationMode": "Linear"
        },
        
        "curveDefinition": {
            "currency": "EUR",
            "indexName":"EURIBOR",
            "discountingTenor": "OIS",
            "indexTenors":["6M"]
        }
    }],
    
    "outputs":["Constituents"]
}
 
response = zcCurve_endpoint.send_request(
    method = rdp.Endpoint.RequestMethod.POST,
    body_parameters = request_body
)

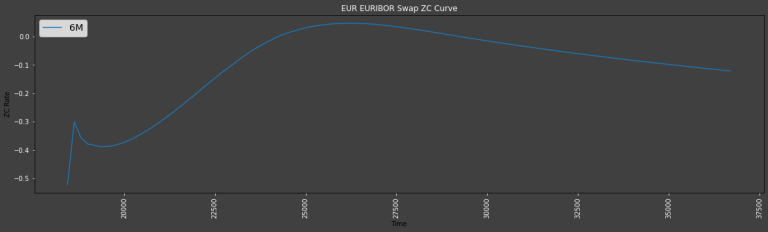
Which produces something like the following i.e.:

The full set of Curve Parameters and Definition used to produce the curve
Curve point data for each available Tenor
List of Constituents

    	
            {
  "data": [
    {
      "curveParameters": {
        "extrapolationMode": "Linear",
        "interpolationMode": "CubicSpline",
        "interestCalculationMethod": "Dcb_Actual_Actual",
        "priceSide": "Mid",
        "calendarAdjustment": "Calendar",
        "calendars": [
          "EMU_FI"
        ],
        "compoundingType": "Compounded",
        "useMultiDimensionalSolver": true,
        "useConvexityAdjustment": true,
        "useSteps": false,
        "convexityAdjustment": {
          "meanReversionPercent": -1.3584,
          "volatilityPercent": 0.474
        },
        "valuationDate": "2020-06-30",
        "ignoreExistingDefinition": false
      },
      "curveDefinition": {
        "availableTenors": [
          "OIS",
          "1M",
          "3M",
          "6M",
          "1Y"
        ],
        "currency": "EUR",
        "mainConstituentAssetClass": "Swap",
        "riskType": "InterestRate",
        "indexName": "EURIBOR",
        "source": "Refinitiv",
        "name": "EUR EURIBOR Swap ZC Curve",
        "id": "9d619112-9ab3-45c9-b83c-eb04cbec382e",
        "discountingTenor": "OIS",
        "indexTenors": [
          "OIS",
          "6M"
        ]
      },
      "curves": {
        "OIS": {
          "curvePoints": [
            {
              "discountFactor": 1.0,
              "endDate": "2020-06-30",
              "ratePercent": -0.5222187504691722,
              "startDate": "2020-06-30",
              "tenor": "0D"
            },
....

....
},
        "6M": {
          "curvePoints": [
            {
              "discountFactor": 1.0,
              "endDate": "2020-06-30",
              "ratePercent": -0.5222187504691722,
              "startDate": "2020-06-30",
              "tenor": "0D"
            },
....

....
},
      "constituents": {
        "interestRateInstruments": {
          "EUR": {
            "deposits": [
              {
                "fields": {
                  "bid": {
                    "value": -0.58
                  },
                  "ask": {
                    "value": -0.45
                  }
                },
                "instrumentDefinition": {
                  "instrumentCode": "EUROND=",
                  "template": "EUR",
                  "tenor": "ON"
                },
                "basis": [
                  "1M",
                  "3M",
                  "6M",
                  "1Y",
                  "OIS"
                ]
              },
....

and so on..

Plot the data

If a particular Currency e.g. SEK, has only one curve available, the indexName attribute can be omitted.
Likewise, there are several other parameters where you can override the default to control the results.

Specifying the curve output Tenors

Generating a forward curve built with the market date of Jan 30th, 2021

As well as the Index Tenor, we provide the Start Tenor and the Tenors we wish to generate the Forward Curve for and use the Forward Curves Endpoint we defined towards the start of the article.

    	
            request_body={
    "universe":[
        {
            "curveDefinition": {
                "currency": "JPY",
                "indexName": "LIBOR",
               "discountingTenor": "1M"
              },
            
            "curveParameters":{
            "valuationDate":"2021-01-30"
            },
 
            "forwardCurveDefinitions": [
                  {
                      "indexTenor": "1M",
                      "forwardStartTenor":"2D",
                      "forwardCurveTenors": ["0M","1M","2M","3M","4M","5M","6M","7M","8M","9M","10M","11M","12M","13M","14M","15M","16M","17M","18M","19M","20M","21M","22M","23M","24M","25M","26M","27M","28M","29M","30M","31M","32M","33M","34M","35M","36M","37M","38M","39M","40M","41M","42M","43M","44M","45M","46M","47M","48M","49M","50M","51M","52M","53M","54M","55M","56M","57M","58M","59M","60M","61M"]
                  }
              ]
        }
    ]
}
 
response = forward_zcCurve_endpoint.send_request(
    method = rdp.Endpoint.RequestMethod.POST,
    body_parameters = request_body)

The response from which looks like:

    	
            {
  "data": [
    {
      "curveParameters": {
        "interestCalculationMethod": "Dcb_Actual_Actual",
        "priceSide": "Mid",
        "calendarAdjustment": "Calendar",
        "calendars": [
          "JAP_FI"
        ],
        "compoundingType": "Compounded",
        "useConvexityAdjustment": true,
        "useSteps": false,
        "valuationDate": "2021-01-30",
        "ignoreExistingDefinition": false
      },
      "curveDefinition": {
        "availableTenors": [
          "6M",
          "OIS",
          "3M",
          "1M"
        ],
        "currency": "JPY",
        "mainConstituentAssetClass": "Swap",
        "riskType": "InterestRate",
        "indexName": "LIBOR",
        "source": "Refinitiv",
        "name": "JPY LIBOR Swap ZC Curve",
        "id": "cbf84acf-5328-4efc-8d23-f476ac495d82",
        "discountingTenor": "1M"
      },
      "forwardCurves": [
        {
          "curvePoints": [
            {
              "discountFactor": 1.000002876383664,
              "endDate": "2021-02-03",
              "ratePercent": -0.05262389411501145,
              "startDate": "2021-02-01",
              "tenor": "0M"
            },
            {
              "discountFactor": 1.0000474669650439,
              "endDate": "2021-03-03",
              "ratePercent": -0.057733431373796495,
              "startDate": "2021-02-01",
              "tenor": "1M"
            },
....

truncated

....
            {
              "discountFactor": 1.0054496613870654,
              "endDate": "2026-03-03",
              "ratePercent": -0.106882246394846,
              "startDate": "2021-02-01",
              "tenor": "61M"
            }
          ],
          "forwardCurveTag": "2DForward",
          "forwardStart": "2D",
          "indexTenor": "1M"
        }
      ]
    }
  ]
}

Implied Foreign Currencies / Currency Adjusted ZC Curves

Here I am using the referenceCurveDefinition parameter to calculate a JPY curve currency adjusted for the USD using LIBOR i.e. integrate currency basis swap, starting with the USD Libor as the reference curve.

    	
            request_body={
    "universe": [
        {
            "curveDefinition": {
                "currency":"JPY",
                "indexName":"LIBOR",
                "discountingTenor": "6M",
                "referenceCurveDefinition": {
                    "currency":"USD",
                    "indexName":"LIBOR",
                    "mainConstituentAssetClass":"Swap",
                    "discountingTenor": "6M",
                }
            }            
        }]
}
 
response = zcCurve_endpoint.send_request(
    method = rdp.Endpoint.RequestMethod.POST,
    body_parameters = request_body
)

Where the response payload looks something like:

    	
            {
  "data": [
    {
      "curveParameters": {
        "extrapolationMode": "None",
        "interpolationMode": "CubicDiscount",
        "interestCalculationMethod": "Dcb_Actual_Actual",
        "priceSide": "Mid",
        "calendarAdjustment": "Calendar",
        "calendars": [
          "JAP_FI"
        ],
        "compoundingType": "Compounded",
        "useMultiDimensionalSolver": true,
        "useConvexityAdjustment": true,
        "useSteps": false,
        "convexityAdjustment": {
          "meanReversionPercent": -6.9637,
          "volatilityPercent": 0.142
        },
        "valuationDate": "2021-05-17",
        "ignoreExistingDefinition": false,
        "referenceCurveParameters": {
          "priceSide": "Mid",
          "calendarAdjustment": "Calendar",
          "compoundingType": "Compounded",
          "useMultiDimensionalSolver": true,
          "useConvexityAdjustment": true,
          "useSteps": false,
          "convexityAdjustment": {
            "meanReversionPercent": 1.1128,
            "volatilityPercent": 0.786
          }
        }
      },
      "curveDefinition": {
        "availableTenors": [
          "OIS",
          "1M",
          "3M",
          "6M"
        ],
        "currency": "JPY",
        "mainConstituentAssetClass": "Swap",
        "riskType": "InterestRate",
        "indexName": "LIBOR",
        "source": "Refinitiv",
        "name": "JPY LIBOR Swap ZC Curve",
        "id": "cbf84acf-5328-4efc-8d23-f476ac495d82",
        "discountingTenor": "6M",
        "indexTenors": [
          "6M"
        ],
        "referenceCurveDefinition": {
          "availableTenors": [
            "OIS",
            "1M",
            "3M",
            "6M"
          ],
          "currency": "USD",
          "mainConstituentAssetClass": "Swap",
          "riskType": "InterestRate",
          "indexName": "LIBOR",
          "source": "Refinitiv",
          "name": "USD LIBOR Swap ZC Curve",
          "id": "1ef0692f-1cde-4b71-bad7-e39198633e0e",
          "discountingTenor": "6M"
        }
      },
      "curves": {
        "6M": {
          "curvePoints": [
            {
              "discountFactor": 1.0,
              "endDate": "2021-05-17",
              "ratePercent": 0.010324072879575041,
              "startDate": "2021-05-17",
              "tenor": "0D"
            },
            {
              "discountFactor": 0.9999991514902243,
              "endDate": "2021-05-20",
              "ratePercent": 0.010324072879575041,
              "startDate": "2021-05-17",
              "tenor": "3D"
            },

....

truncated

....

{
              "discountFactor": 0.5109265114013352,
              "endDate": "2071-05-18",
              "ratePercent": 1.3520439922922955,
              "startDate": "2021-05-17",
              "tenor": "50Y",
              "instruments": [
                {
                  "instrumentCode": "GBPCBS50Y=ICAP",
                  "value": 10.25
                }
              ]
            }
          ],
          "isDiscountCurve": true
        }
      }
    }
  ]
}

Taking collateral currency into account

Similarly, we can use a Pivot Curve - so for example, instead of going directly from EUR to JPY, we can go via USD.

    	
            request_body={
    "universe": [
        {
            "curveDefinition": {
                "currency":"JPY",
                "indexName":"LIBOR",
                "discountingTenor": "OIS",
                "pivotCurveDefinition":{
                    "currency":"USD",
                    "indexName":"LIBOR",
                    "mainConstituentAssetClass":"Swap",
                    "discountingTenor": "OIS"
                },
                "referenceCurveDefinition": {
                    "currency":"EUR",
                    "indexName":"ESTR",
                    "discountingTenor": "OIS"
                }
            }           
        }]
}
 
response = zcCurve_endpoint.send_request(
    method = rdp.Endpoint.RequestMethod.POST,
    body_parameters = request_body
)

User defined ZC Curves

So far I have requested Refinitiv defined Curves and illustrated how you can use parameters to customise the generated output.
However, one of the other great features of the Zero Coupons APIs is that you can define your own ZC Curves by specifying your own constituents.
You will have noted that when I requested a Refinitiv defined curve, the response included the constituents used to generate the curve. So, if required you can take one of our existing curves and modify the constituents and parameter to generate your own custom curve - for example:(following is heavily truncated - you can find the full definition in the accompanying Jupyter Notebook).

    	
             "universe": [


    {
      "curveParameters": {
        "ignoreExistingDefinition": True,
        "valuationDate": "2021-02-23"
      },
      "curveDefinition": {
        "currency": "EUR",
        "discountingTenor": "OIS"
      },
      "constituents": {
        "interestRateInstruments": {
          "EUR": {
            "deposits": [
              {
                "instrumentDefinition": {
                  "instrumentCode": "EUROND=",
                  "template": "EUR",
                  "tenor": "ON"
                },
                "basis": [
                  "6M",
                  "1Y",
                  "3M",
                  "OIS",
                  "1M"
                ]
              },
              {
                "instrumentDefinition": {
                  "instrumentCode": "EURTND=",
                  "template": "EUR",
                  "tenor": "TN"
                },
                "basis": [
                  "6M",
                  "1Y",
                  "3M",
                  "OIS",
                  "1M"
                ]
              },
              {
                "instrumentDefinition": {
                  "instrumentCode": "EURIBOR1YD=",
                  "template": "EUR",
                  "tenor": "1Y"
                },
                "basis": [
                  "1Y"
                ]
              }
            ],
            "fras": [
              {
                "instrumentDefinition": {
                  "instrumentCode": "EUR4X10F=SMKR",
                  "template": "EURFRA",
                  "tenor": "4X10"
                },
                "basis": [
                  "6M"
                ]
              },
              {
                "instrumentDefinition": {
                  "instrumentCode": "EUR0X1F=SMKR",
                  "template": "EURFRA",
                  "tenor": "0X1"
                },
                "basis": [
                  "1M"
                ]
              },
....
....
            ],
            "futures": [
              {
                "basis": [
                  "3M"
                ],
                "instrumentDefinition": {
                  "instrumentCode": "FEIcm8",
                  "template": "FEI"
                }
              },
              {
                "basis": [
                  "3M"
                ],
                "instrumentDefinition": {
                  "instrumentCode": "FEIcm1",
                  "template": "FEI"
                }
              },
....
....
            ],
            "interestRateSwaps": [
              {
                "instrumentDefinition": {
                  "instrumentCode": "EURAB3E14Y=TWEB",
                  "template": "EUR_AB3E",
                  "tenor": "14Y"
                },
                "basis": [
                  "3M"
                ]
              },
              {
                "instrumentDefinition": {
                  "instrumentCode": "EURAB6E8Y=TWEB",
                  "template": "EUR_AB6E",
                  "tenor": "8Y"
                },
                "basis": [
                  "6M"
                ]
              },
....
....
            ],
            "overnightIndexSwaps": [
              {
                "instrumentDefinition": {
                  "instrumentCode": "EUREON11Y=ICAP",
                  "template": "OIS_EONIA",
                  "tenor": "11Y"
                },
                "basis": [
                  "OIS"
                ]
              },
              {
                "instrumentDefinition": {
                  "instrumentCode": "EUREON9M=ICAP",
                  "template": "OIS_EONIA",
                  "tenor": "9M"
                },
                "basis": [
                  "OIS"
                ]
              },
....
....
            ],
            "tenorBasisSwaps": [
              {
                "instrumentDefinition": {
                  "instrumentCode": "EUR6E12E5Y=ICAP",
                  "template": "LBOTH CROSS:EUR CLDR:EMU SETTLE:2WD LRECEIVED LTYPE:FLOAT CUR:EUR CFADJ:Y CCM:MMA0 DMC:M EMC:S FRQ:1 PDELAY:0 LPAID LTYPE:FLOAT CUR:EUR CFADJ:Y CCM:MMA0 DMC:M EMC:S FRQ:2 PDELAY:0",
                  "tenor": "5Y"
                },
                "basis": [
                  "1Y"
                ]
              },
              {
                "instrumentDefinition": {
                  "instrumentCode": "EUR6E12E12Y=ICAP",
                  "template": "LBOTH CROSS:EUR CLDR:EMU SETTLE:2WD LRECEIVED LTYPE:FLOAT CUR:EUR CFADJ:Y CCM:MMA0 DMC:M EMC:S FRQ:1 PDELAY:0 LPAID LTYPE:FLOAT CUR:EUR CFADJ:Y CCM:MMA0 DMC:M EMC:S FRQ:2 PDELAY:0",
                  "tenor": "12Y"
                },
                "basis": [
                  "1Y"
                ]
              },
....
....
              {
                "instrumentDefinition": {
                  "instrumentCode": "EUR1E3E3Y=ICAP",
                  "template": "LBOTH CROSS:EUR CLDR:EMU SETTLE:2WD LRECEIVED LTYPE:FLOAT CUR:EUR CFADJ:Y CCM:MMA0 DMC:M EMC:S FRQ:4 PDELAY:0 LPAID LTYPE:FLOAT CUR:EUR CFADJ:Y CCM:MMA0 DMC:M EMC:S FRQ:12 PDELAY:0",
                  "tenor": "3Y"
                },
                "basis": [
                  "1M"
                ]
              }
            ]
          }
        }
      }
    }
  ],
  "outputs": [
    "DetailedCurvePoint",
    "Constituents"
  ]
}

The response from the above is quite long (even if I were to truncate to highlight the key outputs), so I will omit here - but it is included in the accompanying Jupyter Notebook.

Financial Contracts API

Whilst the main focus of this article is Zero Coupon, I felt it would be remiss of me to not to briefly mention the related IPA Financial Contracts API - which may also of be some interest.

As with the ZC Curves API, we need to know the endpoint URL:

    	
            financial_contract_endpoint = rdp.Endpoint(session, 
    'https://api.refinitiv.com/data/quantitative-analytics/v1/financial-contracts')

Interest Rate swap examples

With the above ZC examples, I showed how you could request a particular curve and use the data in your own application.
However, by using the Financial Contracts API, you can describe an instrument and the apppropriate curves will be fetched behind the scenes.
So, for example, if I want to request a vanilla AUD Interest Rate Swap based on the BBSW index, I need to:

specify the fields that I want calculated
define the instrument to be calculated in terms of the available documented parameters

    	
            request_body = {
    
    "fields" : ["InstrumentTag","MarketValueInDealCcy","DirtyPricePercent",
    "FixedRatePercent", "DiscountCurveName","ForwardCurveName",
    "ErrorCode","ErrorMessage"],
    
    "universe" : [
        {
            "instrumentType":"Swap",
            "instrumentDefinition": {
                "instrumentTag":"IRS-EUR EURIBOR 6M - 5Y",
                "startDate":"2020-07-29",
                "tenor":"5Y",
                "legs":[
                {
                    "direction":"Paid",
                    "interestType":"Fixed",
                    "notionalCcy":"EUR",
                    "interestPaymentFrequency":"Annual",
                    "interestCalculationMethod":"Dcb_Actual_365",
                },
                {
                    "direction":"Received",
                    "interestType":"Float",
                    "interestPaymentFrequency":"SemiAnnual",
                    "interestCalculationMethod":"Dcb_Actual_365",
                    "notionalCcy":"EUR",
                    "indexName":"EURIBOR",
                    "indexTenor":"6M",
                }]
            }
        }],
    
    "pricingParameters": {
        "valuationDate": "2020-7-27T00:00:00Z",
    },
        
    "outputs" : ["Data","Headers"],
 
}
 
response = financial_contract_endpoint.send_request(
    method = rdp.Endpoint.RequestMethod.POST,
    body_parameters = request_body)

If I then convert the response to a Dataframe it looks like this:

InstrumentTag	MarketValueInDealCcy	DirtyPricePercent	FixedRatePercent	DiscountCurveName	ForwardCurveName
IRS-EUR EURIBOR 6M - 5Y	-18956.445802	-1.895645	-0.374483	EUR - Swap vs 6M Euribor	None
IRS-EUR EURIBOR 6M - 5Y	-18956.445802	-1.895645	NaN	EUR - Swap vs 6M Euribor	EUR - Swap vs 6M Euribor

As you will note from the 5th & 6th columns, the response provided details of the underlying curves used to calculate the requested Interest Rate Swap.

I hope the above has provided a useful insight into the power of the Zero Coupon Curve APIs that form part of the broader Instrument Pricing Analytics APIs umbrella.

If you have any questions, please feel free to post on the Refinitiv Developer Community Forums or create a Content support ticket specifically for the Instrument Pricing Analytics product on My.Refinitiv.

Acknowledgements

Although I modified the code for the plots in this article to improve their look and format, the starting point was Samuel Schwalm's Surfaces and Curves notebook - for which I thank him. I would also like to thank Lamya Mrani Alaoui for her help in modifying some of the Curve requests.

Additional Resources

You will find links to the Source code, APIs, Documentation and Related Articles in the Links Panel

Disclaimer

This article was based on earlier API versions, therefore, the method signatures, data formats may have changed - please refer to the latest IPA documentation for current versions.

Zero-Coupon Curves Notebook

Explore all APIs

Explore all Articles

Articles

Developer Tools

Use Cases

Upcoming Events

Past Events

About Us

Instrument Pricing Analytics - Zero-Coupon Curves

Initialisation

Connect to the Refinitiv Data Platform

Endpoint Interface

Identifying the Surfaces Endpoint

Define our API Endpoints for the ZC Curve definitions and ZC Curves data

Querying Curve Definitions

Filtering the list of Curve Definitions

Requesting a curve by its ID

Detailed Response - curve points data - Definition + Parameters

Plot the data

Requesting Curve using Parameters

Plot the data

Specifying the curve output Tenors

Generating a forward curve built with the market date of Jan 30th, 2021

Implied Foreign Currencies / Currency Adjusted ZC Curves

Taking collateral currency into account

User defined ZC Curves

Financial Contracts API

Interest Rate swap examples

Acknowledgements

Additional Resources

Disclaimer

SOURCE CODE ON GITHUB

Related APIs

Related Articles