Author:

Our previous article explained what Net Present Values, Face Values, Maturities, Coupons, and risk-free rates are, how to compute them, and how they are used to calculate excess returns using only Zero-Coupon Bonds; in this article, we look at Coupon Paying Bonds, particularly Cash Flow incurred by Coupons, Bootstrapping and particularities about Sovereign Bond data. Very little is changed in this article until the 'Coupon Paying Rate' section. It is aimed at academics from undergraduate level up, and thus will explain all mathematical notations to ensure that there is no confusion and so that anyone - no matter their expertise on the subject - can follow.
One may find many uses for the methods outlined below. For example: To calculate metrics such as the Sharpe-Ratio, one needs first to calculate excess returns, that then necessitates the calculation of risk-free rates of return.
You may find recordings of my Live Coding Sessions on my YouTube Playlist and Chanel where I explain the code and concepts below.
Webinar Video
This Webinar was broadcasted live on Twitch where I code live every Tuesday at 4pm GMT.
Using this Site
You may use the links below to reach out to contents, and scale up or down the math figures at your convenience as per the below.
Content
- Use of Government Bonds in calculating risk-free rates
- YTM implied daily risk-free rate
- Bootstrapping and Spot-Rates/Discount-Factors: Coupon-Paying Bond's Zero-Coupon Equivalent Yield To Maturity
- Risk-free rates from Spot Rates of Coupon-Paying-Bonds
- Excess Returns from Spot Rates of Coupon-Paying-Bonds
- Conclusion
- References
Use of Government Bonds in calculating risk-free rates
As afformentioned in our previous article, only certain banks have access to the primary sovereign bond markets where they may purchase Domestic Sovereign/Government Bonds. There are many such types of bonds. Among others, there are:
- United States (US): US Treasury securities are issued by the US Department of the Treasury and backed by the US government.
- Fixed principal: A principal is the amount due on a debt. In the case of bonds, it is often referred to as the Face Value. The Face Value of all US Treasury securities is 1000 US Dollars (USD)
- Treasury‐bills (as known as (a.k.a.): T-bills) have a maturity of less than a year (< 1 yr). These are bonds that do not pay coupons (Zero-Coupon Bonds).
- Treasury‐notes (a.k.a.: T‐notes) have a maturity between 1 and 10 years (1‐10 yrs).
- Treasury-bonds (a.k.a.: T‐bonds) have a maturity between 10 and 30 years (10‐30 yrs). It is confusing calling a sub-set of bonds 'T-bonds', but that is their naming conventions. To avoid confusion, I will always refer to them explicitly as Treasury-bonds (or T‐bonds), not just bonds.
- Inflation‐indexed: TIPS
- Treasury STRIPS (created by private sector, not the US government)
- Fixed principal: A principal is the amount due on a debt. In the case of bonds, it is often referred to as the Face Value. The Face Value of all US Treasury securities is 1000 US Dollars (USD)
- United Kingdom: Since1998, gilts have been issued by the UK Debt Management Office (DMO), an executive agency of the HMT (Her Majesty's Treasury).
- Conventional gilts: Short (< 5 yrs), medium (5‐15 yrs), long (> 15 yrs)
- Inflation-indexed gilts
- Japan
- Medium term (2, 3, 4 yrs), long term (10 yrs), super long term (15, 20 yrs)
- Eurozone government bonds
There are several ways to compute risk-free rates based on bonds. In this article, we will focus on T-bills, as US Sovereign Bonds are often deemed the safest (which is a reason why the USD is named the world's reserve currency) and T-bills are an example of Zero-Coupon Bonds (as per the method outlined by the Business Research Plus). From there, a risk-free rate of return can be computed as implied by its bond's Yield To Maturity and based the change in the same bond's market price from one day to the next.
A bond is a debt; a debt with the promise to pay a Face Value ($FV$) in $m$ years (m for maturity) in the future as well as Coupons (summing to $C$ every year) for an amount today. That latter amount paid for the bond may be fair; a fair value at time of the Bond's issue ($t$) is calculated as its Net Present Value ($NPV$) such that:
where $YTM$ is the annualised Yield To Maturity of the Bond in question and $f_{\text{acf}}$ is the annual compound frequency (such that if we compound cash flows annually, $f_{\text{acf}} = 1$; and if we compound cash flows bi-annually (i.e.: twice a year / every 6 months), $f_{\text{acf}} = 0.5$). In this article, we will follow the Refinitiv Adfin calculation for YTM under 'Bond Calculators>Bond Calculator (Premium)>Yield and Yield Curves>Yield Calculation Methods>Adfin Analytics: Price/Yield Calculations>Adfin Bonds>Calculation Guides>Refinitiv Adfin Bonds Calculation Guide>Calculation Price and Yield>Price/Yield Relationship>Yield Calculation'.
Annual Coupon Payment Frequency
Coupons are paid at a fixed 'annual Coupon payment frequency' ($f_{ac \mathbf{p} f}$). Usually, the following are true:
- $f_{ac \mathbf{p} f} = 0.5$, i.e.: Coupon payments are made every 6 months (i.e.: semi-annually)
- $f_{\text{acf}}$ is set to the $f_{ac \mathbf{p} f}$ such that $f_{ac \mathbf{p} f} = f_{ac \mathbf{p} f}$
- Thus $f_{acf} = f_{ac \mathbf{p} f} = 0.5$.
Sub-Annual Interpolation of YTMs
Note that when using YTM values inter-year (e.g.: after 6 month), we then use a fraction of it, i.e.: $f_{\text{acf}} \text{ } YTM$. This is because all YTM values are annualised and - in accounting standards - sub-annual interpolation of YTMs are always linear/arithmetic. It must be remembered - however - that super-annual (i.e.: more than a year) extrapolation of YTMs are not necessarily linear/arithmetic.
Compounding
It follows from the above that if $f_{\text{acf}} = 1$ such that we use an annually compounding accounting method, annual extrapolation of YTMs are geometric.
Since Coupons are most often paid bi-annually, it is common standard to compound cashflows bi-annually too when they involve Bonds - as aforementioned. This is done to model a Bond-holding-agent) who re-invests Coupon payments as soon as they're received. In this scenario, $f_{acf} = f_{ac \mathbf{p} f} = 0.5$.
Discount Factor
It is easy to see that NPVs and YTMs are therefore (inversely) related; if one changes, the other must change too. We may - therefore - equivalently speak about a change in NPV and a change in YTM since the FV (for each sovereign bond issuer) does not change. The YTM acts as the discount factor here; as a matter of fact, we can see that the YTM is the annual growth rate of our NPV that leads it to the FV in the following:
Comparability
NPVs of different bonds are not comparable. That is because they account for bonds maturing at different times. Instead, YTMs of different bonds are comparable because they are annualised, therefore they account for different maturities. It is thus preferable to only speak of changes in sovereign bond NPVs in terms of the change in their YTMs; then we can compare them to each other, e.g.: in a Yield Curve (that can be seen here with Refinitiv credentials):
T-Note Example: Five Year T-Note with Semi-Annual Compounding
Using a semi-annual compounding accounting method (such that $f_{\text{acf}} = 0.5 = f_{\text{acpf}}$), a T-Note that matures in 5 Years (Five-Year T-Bill, FYTN) has a Net Present Value (${NPV}_{\text{FYTN}, f_{\text{acf}}, t}$) of ${NPV}_{\text{FYTN}, 0.5, t}$ at time t such that:
Let's have a look at data from "2020-07-31":
# We need to gather our data. Since Refinitiv's DataStream Web Services (DSWS) allows for access to the most accurate and wholesome end-of-day (E.O.D.) economic database (DB), naturally it is more than appropriate. We can access DSWS via the Python library "DatastreamDSWS" that can be installed simply by using pip install .
import DatastreamDSWS as DSWS
# We can use our Refinitiv's Datastream Web Socket (DSWS) API keys that allows us to be identified by Refinitiv's back-end services and enables us to request (and fetch) data:
DSWS_username = open("Datastream_username.txt", "r") # The username is placed in a text file so that it may be used in this code without showing it itself
DSWS_password = open("Datastream_password.txt", "r") # Same for the password
ds = DSWS.Datastream(username=str(DSWS_username.read()),
password=str(DSWS_password.read()))
# It is best to close the files we opened in order to make sure that we don't stop any other services/programs from accessing them if they need to:
DSWS_username.close()
DSWS_password.close()
# Now let's get US Treasury Note (Maturing) 31/07/25:
fytn_Coupon_2020_07_31_p = ds.get_data( # the ' _p ' is for 'price'
tickers='613XGU', # found this ticker on https://product.datastream.com/browse/search.aspx?dsid=ZRQW955&AppGroup=DSAddin&q=US+Treasury+Note+31%2F07%2F25&prev=99_US+Treasury+Note+(Maturing)+31%2F07%2F25&nav_category=13
start = "2020-07-29", fields="X", freq='D')
fytn_Coupon_2020_07_31_p.dropna().T
| Dates | 29/07/2020 | 30/07/2020 | 31/07/2020 | 03/08/2020 | 04/08/2020 | 05/08/2020 | 06/08/2020 | 07/08/2020 | 10/08/2020 | 11/08/2020 | ... | 05/08/2021 | 06/08/2021 | 09/08/2021 | 10/08/2021 | 11/08/2021 | 12/08/2021 | 13/08/2021 | 16/08/2021 | 17/08/2021 | 18/08/2021 | |
| Instrument | Field | |||||||||||||||||||||
| 613XGU | X | 99.9765 | 100.1016 | 100.2031 | 100.1484 | 100.2891 | 100.1328 | 100.1719 | 100.1016 | 100.0625 | 99.8672 | ... | 98.7109 | 98.5469 | 98.4688 | 98.3515 | 98.4375 | 98.3672 | 98.5469 | 98.5859 | 98.5547 | 98.5625 |
fytn_Coupon_2020_07_31_p.loc["2020-07-30"]
Instrument Field
613XGU X 100.1016
Name: 2020-07-30, dtype: float64
We can see that the price on "2020-07-31" was \$100.1016, so it was selling at a premium. We are using '613XGU' instead of 'TRUS5YT' as the latter is the YTM given for sovereign-provided bonds which one cannot actually buy - only investment banks can purchase such bonds. (Many pension funds and asset managers hold sovereign bonds, but investment banks are the institutions who trade them.) Here instead we are looking at sovereign bonds sold by the investment bank 'Deutsche Boerse AG'. This means that, in our equation, we'd use the realised price of \$100.1016 instead of the ${NPV}_{\text{FYTN}, 0.5, "2020-07-31"}$.
# Now let's get US Treasury Note (Maturing) 31/07/25:
fytn_Coupon_2020_07_31_f = ds.get_data( # the ' _f ' is for 'fixed', as in fixed data.
tickers='613XGU', # found this ticker on https://product.datastream.com/browse/search.aspx?dsid=ZRQW955&AppGroup=DSAddin&q=US+Treasury+Note+31%2F07%2F25&prev=99_US+Treasury+Note+(Maturing)+31%2F07%2F25&nav_category=13
kind=0, # ' kind=0 ' is needed here as we are looking for static data that doesn't change with time.
fields=["NAME", "ID", "TERM", "RV", "C", "CTYP", "RDL", "EXCHB", "DEF",
"MPD.U", "BTYP", "AIS", "BAB"])
fytn_Coupon_2020_07_31_f.T
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| Instrument | 613XGU | 613XGU | 613XGU | 613XGU | 613XGU | 613XGU | 613XGU | 613XGU | 613XGU | 613XGU | 613XGU | 613XGU | 613XGU |
| Datatype | NAME | ID | TERM | RV | C | CTYP | RDL | EXCHB | DEF | MPD.U | BTYP | AIS | BAB |
| Value | US TREASURY NOTE 2020 1/4% 31/07/25 AB-2025 | 31/07/2020 | 5 | 100 | 0.25 | FIX | 31/07/2025 | FF MU DD | MPD | % | STR | 54568290 | 5 |
| Dates | 18/08/2021 | 18/08/2021 | 18/08/2021 | 18/08/2021 | 18/08/2021 | 18/08/2021 | 18/08/2021 | 18/08/2021 | 18/08/2021 | 18/08/2021 | 18/08/2021 | 18/08/2021 | 18/08/2021 |
From the above we can note that the Issuing Date (ID) is 2020-07-31 with a maturity (also known as (a.k.a.) Term) of 5 years, thus a Last Redemption Date (RDL) of 2025-07-31, a Face Value (a.k.a. "Redemption Value" - RV) of \$100, and a Fixed Coupon Rate of 0.25% - which is quite low. We have a Straight (cash flows are fixed) (```BTYP```) debt of which 54568290 (```AIS```) was sold in the currency and time of issue with daily accrural basis. (We can also see the exchanges where our security was listed, shown as Codes.) It is unusual to have T‐notes with Face Values other than \$1000, but this is hat we're dealing with here. We thus now have:
since
0.5 * (0.25/100) * 100
0.125
Thus:
$$ \begin{array}{ll} 0 &= \frac{FV_{\text{FYTN}, "2020-07-31"}}{\left(1 + 0.5 \text{ } YTM_{\text{FYTN}, "2020-07-31"}\right)^{10}} + \sum^{10}_{\tau=1} {\frac{0.5 \text{ } \mathcal{C}_p \text{ } \text{ } FV_{\text{FYTN}, "2020-07-31"}}{ (1 + 0.5 \text{ } YTM_{\text{FYTN}, "2020-07-31"})^{\tau} }} - \text{\$}100.1016 & \text{ as per the above} \\ &= \frac{\text{\$}100}{\left(1 + 0.5 \text{ } YTM_{\text{FYTN}, "2020-07-31"}\right)^{10}} + \sum^{10}_{\tau=1} {\frac{\text{\$}0.125}{ (1 + 0.5 \text{ } YTM_{\text{FYTN}, "2020-07-31"})^{\tau} }} - \text{\$}100.1016 & \text{ as per the above} \\ &\approx \frac{\text{\$}100}{\left(1 + 0.5 \text{ } * \text{ } 0.002295515059055049 \right)^{10}} + \sum^{10}_{\tau=1} {\frac{\text{\$}0.125}{ (1 + 0.5 \text{ } * \text{ } 0.002295515059055049)^{\tau} }} - \text{\$}100.1016 \end{array}$$as computed iteratively with the Python function YTM_Solver defined bellow:
ytm_op = YTM_Solver(fv=100, c=0.25, m=5, p=100.1016, f_acf=0.5, details=True)['Opt. YTM']
print(f"Our optimal YTM is {ytm_op}")
remainder: 0.0, m: 5.0, m_rounded: 5.0
It is most likely that if ' remainder ' is 0, we're looking at a newly issued Bond, in which case we're not going to get a coupon payment at time '0'. If you do expect a coupon payment straight away, then please specify it in arguments ' cash_flow_no_fv ' or ' cash_flow_with_fv '.
Years to each Coupon Payments (len: 10): [0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0]
0.5 year periods to each Coupon Payments (len: 10): [1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0]
Cashflow (len: 10): [0.125, 0.125, 0.125, 0.125, 0.125, 0.125, 0.125, 0.125, 0.125, 100.125]
Our optimal YTM is 0.002295515059055018
Checking the error manually to verify sound mathematics in the YTM_Solver function:
(100/((1+(0.5*ytm_op))**(10))) - 100.1016 + (sum(
[0.125/((1 + (0.5 * ytm_op))**(i)) for i in range(1, 11)]))
1.2434497875801753e-14
Computing Series of YTM Values
We cannot use the same price data from fytn_Coupon_2020_07_31_p through time along with the YTM_Solver to construct a data-frame of ytms of interest. This is because the maturity technically is different every day, decreasing by a day every time-period/row. Instead, we need a new Bond with the same maturity per row of our series.
Searching the Datastream Navigator Programmatically with DSWS
Using DS.SYMBOLLOOKUP(Category=Bonds & Convertibles) as a field of ds.get_data, we can search for our Bonds of interest (i.e.: 5 year US Bonds) within any period of interest (e.g.: 2022 to 2027). But 1st, there are some Python libraries we need to import:
# There are some libraries we need to import:
import pandas # pandas will be needed to manipulate data sets
from datetime import datetime
import calendar
print("The pandas library imported in this code is version: " + pandas.__version__)
The pandas library imported in this code is version: 1.2.4
We also need to construct Python functions DSWS_fixed_data_collection and DSWS_fixed_and_price_data_collection_and_ytm that collects required data from Datastream. Now we can now start searching the Datastream Navigator programmatically with DSWS:
# Collect a list of all the relevent Datastream Instrument Codes:
list_of_instrument_dfs, list_of_instruments = [], []
for j in range(2022, 2027): # range from year to year
for i in range(1, 13): # range from month to month
monthrange = calendar.monthrange(j, i) # This gives two numbers in a tuple, the start day of any month (always 1) and the last.
search_term = 'US Treasury Note ' + str(j-5) + ' ' + str( # Our search term is what we are going to look for; imagine we are using the Datastream Navigator and searching for that term. The ' -5 ' is here because we're looking at Bonds with 5 year terms.
monthrange[1]) + '/' + '{:>02}'.format(i) + '/' + str(j)[2:] # ' monthrange[1] ' is the last date of that month. Also, ' '{:>02}'.format(i) ' adds a leading '0' in front of single digits, which is needed in our search term.
instrument = ds.get_data( # This gets the lookup data from Datastream's Navigator's API via the ' DS.SYMBOLLOOKUP ' field.
tickers=search_term, kind=0,
fields=['DS.SYMBOLLOOKUP(Category=Bonds & Convertibles)'])
list_of_instrument_dfs.append(instrument)
if instrument["Value"][0] != "No matches":
list_of_instruments.append(instrument["Instrument"].values[0])
Now we can use them all together:
# Collect original fixed data from DSWS:
ytm_df = DSWS_fixed_and_price_data_collection_and_ytm(instruments=list_of_instruments)
ytm_df
| DSCD | NAME | ID | TERM | RV | C | CTYP | RDL | Price at issue | CD | CF | YTM | |
| 0 | 613XGU | US TREASURY NOTE 2020 1/4% 31/07/25 AB-2025 | 31/07/2020 | 5 | 100 | 0.25 | FIX | 31/07/2025 | 100.2031 | [2021-02-01 00:00:00, 2021-08-02 00:00:00, 202... | [0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.2... | 0.002091 |
| 0 | 616J44 | US TREASURY NOTE 2020 1/4% 31/08/25 AC-2025 | 31/08/2020 | 5 | 100 | 0.25 | FIX | 31/08/2025 | 99.9063 | [2021-03-01 00:00:00, 2021-08-31 00:00:00, 202... | [0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.2... | 0.002689 |
| 0 | 619AX8 | US TREASURY NOTE 2020 1/4% 30/09/25 AD-2025 | 30/09/2020 | 5 | 100 | 0.25 | FIX | 30/09/2025 | 99.8594 | [2021-03-31 00:00:00, 2021-09-30 00:00:00, 202... | [0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.2... | 0.002783 |
| 0 | 622HAG | US TREASURY NOTE 2020 1/4% 31/10/25 AF-2025 | 31/10/2020 | 5 | 100 | 0.25 | FIX | 31/10/2025 | 99.3359 | [2021-04-30 00:00:00, 2021-11-01 00:00:00, 202... | [0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.2... | 0.003842 |
| 0 | 624Z3N | US TREASURY NOTE 2020 3/8% 30/11/25 AG-2025 | 30/11/2020 | 5 | 100 | 0.375 | FIX | 30/11/2025 | 100.0547 | [2021-06-01 00:00:00, 2021-11-30 00:00:00, 202... | [0.375, 0.375, 0.375, 0.375, 0.375, 0.375, 0.3... | 0.00364 |
| 0 | 628GF5 | US TREASURY NOTE 2020 3/8% 31/12/25 AH-2025 | 31/12/2020 | 5 | 100 | 0.375 | FIX | 31/12/2025 | 100.0703 | [2021-06-30 00:00:00, 2021-12-31 00:00:00, 202... | [0.375, 0.375, 0.375, 0.375, 0.375, 0.375, 0.3... | 0.003608 |
| 0 | 6309UZ | US TREASURY NOTE 2021 3/8% 31/01/26 U-2026 | 31/01/2021 | 5 | 100 | 0.375 | FIX | 31/01/2026 | 99.75 | [2021-08-02 00:00:00, 2022-01-31 00:00:00, 202... | [0.375, 0.375, 0.375, 0.375, 0.375, 0.375, 0.3... | 0.004256 |
| 0 | 634DPQ | US TREASURY NOTE 2021 1/2% 28/02/26 V-2026 | 28/02/2021 | 5 | 100 | 0.5 | FIX | 28/02/2026 | 98.875 | [2021-08-31 00:00:00, 2022-02-28 00:00:00, 202... | [0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, ... | 0.007295 |
| 0 | 637QZJ | US TREASURY NOTE 2021 3/4% 31/03/26 W-2026 | 31/03/2021 | 5 | 100 | 0.75 | FIX | 31/03/2026 | 99.0859 | [2021-09-30 00:00:00, 2022-03-31 00:00:00, 202... | [0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.7... | 0.009376 |
| 0 | 6403CY | US TREASURY NOTE 2021 3/4% 30/04/26 Y-2026 | 30/04/2021 | 5 | 100 | 0.75 | FIX | 30/04/2026 | 99.5156 | [2021-11-01 00:00:00, 2022-05-02 00:00:00, 202... | [0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.7... | 0.008492 |
| 0 | 6439UZ | US TREASURY NOTE 2021 3/4% 31/05/26 Z-2026 | 31/05/2021 | 5 | 100 | 0.75 | FIX | 31/05/2026 | 99.8125 | [2021-11-30 00:00:00, 2022-05-31 00:00:00, 202... | [0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.75, 0.7... | 0.007883 |
| 0 | 646V3Q | US TREASURY NOTE 2021 7/8% 30/06/26 AA-2026 | 30/06/2021 | 5 | 100 | 0.875 | FIX | 30/06/2026 | 99.9219 | [2021-12-31 00:00:00, 2022-06-30 00:00:00, 202... | [0.875, 0.875, 0.875, 0.875, 0.875, 0.875, 0.8... | 0.00891 |
Here's an example of one of the cash-flows outputted:
pandas.DataFrame(data=ytm_df['CF'].iloc[0], index=ytm_df['CD'].iloc[0]).T
| 01/02/2021 | 02/08/2021 | 31/01/2022 | 01/08/2022 | 31/01/2023 | 31/07/2023 | 31/01/2024 | 31/07/2024 | 31/01/2025 | 31/07/2025 | |
| 0 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 |
Graph Series with Plotly
We can graph such YTMs or prices simply with the following:
# 1st we need to import some new Python libraries:
from datetime import date, timedelta
import statistics
# The below are needed to plot graphs of all kinds
import plotly
import plotly.express
import plotly.graph_objects as go
from plotly.subplots import make_subplots
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
init_notebook_mode(connected=True)
import cufflinks
cufflinks.go_offline()
# cufflinks.set_config_file(offline = True, world_readable = True)
for i, j in zip(["plotly", "cufflinks"], [plotly, cufflinks]):
print("The " + str(i) + " library imported in this code is version: " + j.__version__)
The plotly library imported in this code is version: 4.14.3
The cufflinks library imported in this code is version: 0.17.3
fig = make_subplots(specs=[[{"secondary_y": True}]]) # Create figure with secondary y-axis
# Create vertical lines when Coupon rates change
c_changed_date, shapes = [], []
for i in range(len(ytm_df)-1):
if ytm_df.iloc[i]["C"] - ytm_df.iloc[i+1]["C"] != 0:
sdate = datetime.strptime(ytm_df.iloc[i]["ID"], '%Y-%m-%d')
edate = datetime.strptime(ytm_df.iloc[i+1]["ID"], '%Y-%m-%d')
delta = edate - sdate
inter_dates = [sdate + timedelta(days=i) for i in range(delta.days + 1)]
c_changed_date.append(inter_dates[int(statistics.median(
range(1, len(inter_dates))))].strftime('%Y-%m-%d'))
for i in c_changed_date:
shapes.append({'type': 'line', 'xref': 'x', 'yref': 'paper',
'x0': i, 'y0': 0, 'x1': i, 'y1': 1})
fig.update_layout(shapes=shapes,)
# Add traces
fig.add_trace(go.Scatter(x=ytm_df["ID"], y=ytm_df["YTM"],
name="Yield To Maturity", line_color="#1f77b4"),
secondary_y=False,)
fig.add_trace(go.Scatter(x=ytm_df["ID"], y=ytm_df["Price at issue"],
name="Price at issue", line_color="#383838"),
secondary_y=True,)
# Set y-axes titles
fig.update_yaxes(title_text="Yield To Maturity", secondary_y=False)
fig.update_yaxes(title_text="Price in US$", secondary_y=True)
fig.update_layout(title_text="US 5 Year T-Note",
yaxis=dict(titlefont=dict(color="#1f77b4"),
tickfont=dict(color="#1f77b4")),)
fig.update_xaxes(title_text="Date") # Set x-axis title
fig.show()
Interestingly here, we can see that YTM and prices don't always move inversely; that's because the Coupon rates are not constant throughout. I thus added vertical lines in-between the dates when Coupon rates change to ease comparisons. Also, we can note that when the price of the Bond goes above its FV (of $100), the YTM does not go negative; that's because of the added revenue from Coupons. If we were looking at a non Coupon paying (i.e.: a Zero-Coupon) Bond, then its YTM would be negative when its price was higher than its FV. Often - as a matter of fact - we do extrapolate Zero-Coupon Equivalent YTMs, this way all YTMs are comparable to each other. This is called 'Bootstrapping)'.
Now, we are going to extrapolate the YTM of any coupon-paying Bond as though it did not pay coupons. To do so, we will need to compute Spot-Rates for each period of interest ($f_{\text{acf}}$), then the Spot-Rate for the period of interest is our Zero-Coupon Equivalent Yield To Maturity ($YTM_{ZCE}$).
Computing $YTM_{ZCE}$ is only useful for Coupon-paying Bonds, so we're only looking at a Coupon-paying Bond. Then the Net Present Value of the Bond of interest at the time of issue is $$ NPV_{{Bond}_t, f_{\text{acf}}} = \begin{Bmatrix} \frac{FV_{Bond}}{\left(1 + f_{\text{acf}} \text{ } {SR}_{{Bond}_t, T}\right)^\frac{m_{Bond}}{f_{\text{acf}}}} + \sum^{^\frac{m_{Bond}}{f_{\text{acf}}}}_{\tau=1} {\frac{f_{\text{acf}} \text{ } C_{{Bond}_t}}{ (1 + f_{\text{acf}} \text{ } {SR}_{{Bond}_t, \tau})^{\tau} }} & \text{if } m_{Bond} \geq f_{\text{acf}} \\ \\ \frac{FV_{Bond} + m_{Bond} \text{ } C_{{Bond}_t}}{\left(1 + \text{ } m_{Bond} \text{ } {SR}_{{Bond}_t, T}\right)} & \text{if } m_{Bond} < f_{\text{acf}} \end{Bmatrix} $$ where
- $T$ is the last time period of interest (it could be $m_{Bond}$ if each time period is a year long) (thus it's always the case that $T = \frac{m_{Bond}}{f_{\text{acf}}}$),
- $f_{\text{acf}}$ is the Annual Compounding Frequency in our accounting method used to calculate $NPV_{{Bond}_t, f_{\text{acf}}}$,
- $Bond$ is the Bond we're interested in, e.g.: $FYTN$ (Five Year Treasury-Note),
- $FV_{Bond}$ is the Face Value of the $Bond$ (usually \$1000 or \$100 when dealing with US sovereign Bonds),
- $m_{Bond}$ is the Maturity of the $Bond$ at time of issue, a.k.a. the Term of the Bond,
- ${Bond}_t$ is the Bond we're interested in specifically issued at time $t$, e.g.: $FYTN_{\text{"2020-01-31"}}$ (Five Year Treasury-Note issued on the 31st of January 2020),
- $ C_{{Bond}_t} = \mathcal{C}_{p,{Bond}_t} \text{ } * \text{ } FV_{Bond}$ where $\mathcal{C}_{p,{Bond}_t}$ is the Coupon rate of ${Bond}_t$ (usually expressed as a persentage (thus the '$p$' of $FV_{Bond}$),
- and ${SR}_{{Bond}_t, \mathtt{t}}$ is the Spot Rate for ${Bond}_t$ at time $\mathtt{t}$. Note that ${SR}_{{Bond}_t, \tau}$ above is in a summation iterating through $\tau$s, meaning that we are using a different ${SR}_{{Bond}_t, \tau}$ for each $\tau$ iteration.
then (with he example of US sovereign Bonds) we don't have to look into Bonds with maturities of 1 year or less (since they don't pay Coupons). Thus ${SR}_{{Bond}_t, \tau}$ for US sovereign Bonds for the 1st year is already known and can be found on Datastream. From these 1st few discoverable Spot Rates, (i) one can figure out the next Spot Rate (the 1st theoretical Spot Rate); (ii) then the 2nd theoretical Spot Rate can be calculated using the discoverable Spot Rates and the 1st theoretical Spot Rate, (iii) then the 3rd theoretical Spot Rate can be calculated using the discoverable Spot Rates and the first two theoretical Spot Rates, and so on till time period '$T$'. Doing so means that we have all ${SR}_{{Bond}_t, \mathtt{t}}$ where $\mathtt{t} > \mathtt{T}$ and $\mathtt{T}$ is the end of the time window investigated at any stage (i), (ii), ... Thus, at any one of these stages we can let $T = \mathtt{T}$; and remembering that $T = \frac{m_{Bond}}{f_{\text{acf}}}$, then:
Let's add 'hats' to the unknown variables; here the only unknown variable is the last ${SR}_{{Bond}_t, \mathtt{t}}$ which is ${SR}_{{Bond}_t, \mathtt{T}}$, so it'll be written as $\widehat{{SR}_{{Bond}_t, \mathtt{T}}}$. Remember that this is because we have all ${SR}_{{Bond}_t, \mathtt{t}}$ where $\mathtt{t} > \mathtt{T}$ and $\mathtt{T}$ is the end of the time window investigated at any stage (i), (ii), ... defined above. Then:
then: $$ \begin{array}{ll} \widehat{{SR}_{{Bond}_t, \mathtt{T}}} &= \frac{ \sqrt[\mathtt{T}]{\frac{FV_{Bond} + f \text{ } C_{{Bond}_t}}{{NPV}_{{Bond}_t, f} - \sum^{^{\mathtt{T}-1}}_{\tau=1} {\frac{f \text{ } C_{{Bond}_t}}{ (1 + f \text{ } {SR}_{{Bond}_t, \tau})^{\tau} }}}} - 1 }{f} \end{array} $$
Let's make a Python function to return this Spot Rate for any such stage:
def Spot_Rate_Last(fv, m, c, p, sr, f=0.5):
"""Spot_Rate_Last(f,fv,m,c,p,sr)
This Python function returns the Zero-Coupon Equivalent rate of a coupon-paying Bond (otherwise known as the Spot-Rate) of one time period (defined as ' f ') after the last one in the list of provided (past) spot-rates (' sp ').
Returns
-------
float: The last spot rate of a Bond for the period looked at.
"""
discouted_coupon_payments = sum([(f*c)/((1 + (f*j))**(i+1)) # ' +1 ' because 'enumerate' starts at 0
for i, j in enumerate(sr)])
last_sr = ((((fv + f*c)/(p - discouted_coupon_payments))**(f/m))-1)/f
return last_sr
Now we can repeat the above for different US T-Notes with similar issue dates and different maturing dates. We collect all data-points in a Python dictionary container_container before tidying it in the yc_df pandas data-frame below. Remember though, we've put ourselves in the shoes of an economic agent looking to invest in 'brand new' sovereign Bonds, in Bonds that our agent would buy on issue; such bonds are called on-the-run sovereign Bonds.
yc_df = DSWS_fixed_and_price_data_collection_and_ytm(
instruments=["613V2R", "613XGW", "613XGU", "613XG1"],
fields=["DSCD", "NAME", "ID", "TERM",
"RV", "C", "CTYP", "RDL"])
yc_df.index = yc_df['RDL']
display(yc_df)
yc_df["YTM"].iplot(title="Yield To Maturity of US Treasury Note issued at end of Jully 2020 with fixed and different Coupon rates")
| DSCD | NAME | ID | TERM | RV | C | CTYP | RDL | Price at issue | CD | CF | YTM | |
| RDL | ||||||||||||
| 29/12/2020 | 613V2R | UTD.STS OF AMERICA 2020 ZERO 29/12/20 | 28/07/2020 | 0.5 | 100 | 0 | ZERO | 29/12/2020 | 99.9469 | [2021-02-01 00:00:00] | [0.0] | 0.001063 |
| 31/07/2022 | 613XGW | US TREASURY NOTE 2020 1/8% 31/07/22 BD-2022 | 31/07/2020 | 2 | 100 | 0.125 | FIX | 31/07/2022 | 100.0313 | [2021-02-01 00:00:00, 2021-08-02 00:00:00, 202... | [0.125, 0.125, 0.125, 0.125] | 0.001093 |
| 31/07/2025 | 613XGU | US TREASURY NOTE 2020 1/4% 31/07/25 AB-2025 | 31/07/2020 | 5 | 100 | 0.25 | FIX | 31/07/2025 | 100.2031 | [2021-02-01 00:00:00, 2021-08-02 00:00:00, 202... | [0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.2... | 0.002091 |
| 31/07/2027 | 613XG1 | US TREASURY NOTE 2020 3/8% 31/07/27 N-2027 | 31/07/2020 | 7 | 100 | 0.375 | FIX | 31/07/2027 | 99.914 | [2021-02-01 00:00:00, 2021-08-02 00:00:00, 202... | [0.375, 0.375, 0.375, 0.375, 0.375, 0.375, 0.3... | 0.003875 |
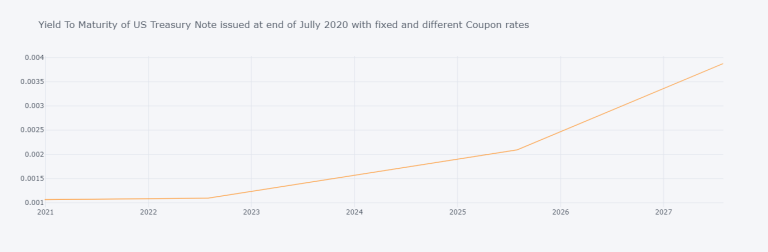
We can see that we have very little liquidity in such on-the-run sovereign Bonds. I couldn't find ones that our agent could buy at time of issue (towards the end of July 2020). Such a lack of liquidity does not provide us with enough data-points to compute Spot Rates.
Example of how a lack in liquidity in on-the-run sovereign Bonds disables us from computing Spot Rates without using off-the-run sovereign Bonds' data
We know from the
yc_dfdata-frame above that we do not have data for on-the-run US Treasury Bonds issued towards the end of July 2020 with 1 year maturity. That's because such a specific Bond is not being sold on the market. Say that we try to compute the Spot Rate for such a specific Bond, we'd have to use the following data:
Maturity (Years) Coupon Rate Price at issue Yield To Maturity 0.5 0 99.9469 0.001063 1 $\mathcal{C}_{p,\text{OYTB}_{"2020-07-31"}}$ $P_{\text{OYTB}_{"2020-07-31"}}$ $YTM_{\text{OYTB}_{"2020-07-31"}}$
Where $P_{\text{OYTB}_{"2020-07-31"}}$ is the price of our fictitious One Year Treasury Bill issued on 2020-07-31. Then our cashflow is:
Time (years) from issue to cashflow date Calculation of discounted cashflow Discounted cashflow 0.5 $\mathcal{C}_{p, \text{OYTB}_{"2020-07-31"}}$ x ${FV}_{\text{OYTB}}$ x $f_{\text{acpf}}$ = 0.000 x \$100 x 0.5 \$0.00 1 $\mathcal{C}_{p, \text{OYTB}_{"2020-07-31"}}$ x ${FV}_{\text{OYTB}}$ x $f_{\text{acpf}} = 0.000$ x \$100 x 0.5 + \$100 \$100 $$ \begin{array}{ll} {NPV}_{\text{OYTB}_{"2020-07-31"}, 0.5} &= \frac{\mathcal{C}_{p, \text{OYTB}_{"2020-07-31"}} \text{ x } {FV}_{\text{OYTB}} \text{ x } f_{\text{acpf}}}{1 + {SR}_{\text{OYTB}_{"2020-07-31"}, 1}} + \frac{\mathcal{C}_{p, \text{OYTB}_{"2020-07-31"}} \text{ x } {FV}_{\text{OYTB}} \text{ x } f_{\text{acpf}} + {FV}_{\text{OYTB}_{"2020-07-31"}}}{(1 + {SR}_{\text{OYTB}_{"2020-07-31"}, 2})^2} \\ P_{\text{OYTB}_{"2020-07-31"}} &= \frac{\mathcal{C}_{p, \text{OYTB}_{"2020-07-31"}} \text{ x } {FV}_{\text{OYTB}} \text{ x } f_{\text{acpf}}}{1 + {SR}_{\text{OYTB}_{"2020-07-31"}, 1}} + \frac{\mathcal{C}_{p, \text{OYTB}_{"2020-07-31"}} \text{ x } {FV}_{\text{OYTB}} \text{ x } f_{\text{acpf}} + {FV}_{\text{OYTB}_{"2020-07-31"}}}{(1 + {SR}_{\text{OYTB}_{"2020-07-31"}, 2})^2} \text{ letting } {NPV}_{\text{OYTB}_{"2020-07-31"}, 0.5} = P_{\text{OYTB}_{"2020-07-31"}} \\ &= \frac{0.000 \text{ x } \$100 \text{ x } 0.5}{1 + {SR}_{\text{OYTB}_{"2020-07-31"}, 1}} + \frac{0.000 \text{ x } \$100 \text{ x } 0.5 + \$ 100}{(1 + {SR}_{\text{OYTB}_{"2020-07-31"}, 2})^2} \\ &= \frac{0.000 \text{ x } \$100 \text{ x } 0.5}{1 + {YTM}_{\text{SMTB}_{"2020-07-31"}}} + \frac{0.000 \text{ x } \$100 \text{ x } 0.5 + \$ 100}{(1 + {SR}_{\text{OYTB}_{"2020-07-31"}, 2})^2} \text{ letting } {SR}_{\text{OYTB}_{"2020-07-31"}, 1} = {YTM}_{\text{SMTB}_{"2020-07-31"}} = \text{ YTM of the Six Month Treasury Bill at time of its issue} \\ &= \frac{\$ 100}{(1 + {SR}_{\text{OYTB}_{"2020-07-31"}, 2})^2} \text{, thus} \\ {SR}_{\text{OYTB}_{"2020-07-31"}, 2} &= \sqrt[2]{\frac{\$ 100}{P_{\text{OYTB}_{"2020-07-31"}}}}-1 \end{array}$$
since the Coupon rate of all US Bonds with maturities equal to or lower than 1 year are Zero-Coupon. Then
And thus, without a OYTB Bond from which to get $P_{\text{OYTB}_{"2020-07-31"}}$, we cannot calculate ${SR}_{\text{OYTB}_{"2020-07-31"}, 2}$.
This lack of on-the-run liquidity can be solved by using off-the-run Bonds:
On and Off-the-run sovereign Bonds
Off-the-run sovereign Bonds are simply Bonds issued before the latest. In our hypothetical situation, we were only looking at Bonds issued at (approximately) the same time, at the end of July 2020. What we can do however, is look at Bonds issued earlier. E.g.: We can use a Bond with 1 year to maturity issued 6 months earlier (at the end of January 2020).
from_date = "2020-07-31"
We stick to 360 days a year to keep in line with the FEDERAL RESERVE statistical release, however, we should both (i) let people chose the average number of days per year they deem useful in this calculation and (ii) the rounding they're ready to use
off_run_df = DSWS_fixed_and_price_data_collection_and_ytm(
instruments=["247DK9", "235FFA", "218QH0", "823D0N", "210EV1",
"235FFD", "247DLH", "218QJQ", "235FF9", "247DLR"],
fields=["DSCD", "NAME", "ID", "TERM",
"RV", "C", "CTYP", "RDL"])
# Configure the data-frame's index appropriately
off_run_df.index = off_run_df['RDL']
off_run_df.index.names = ['RD'] # ' RD ' for Redemption Date
# Combine off- and on-the-run Bonds' data-frames
off_on_df = yc_df.append(off_run_df)
# Collect and add price data as of date of interest
off_on_df["Price on 2020-07-31"] = [
ds.get_data(start="2020-07-31", end="2020-07-31",
fields="X", freq='D',
tickers=i).values[0][2]
for i in list(off_on_df["DSCD"])]
# Add the YTM implied by 2020-07-31 Price
off_on_df["YTM implied by 2020-07-31 Price"] = [
YTM_Solver(
fv=off_on_df.iloc[i]["RV"],
c=off_on_df.iloc[i]["RV"] * off_on_df.iloc[i]["C"] / 100,
m=(round(2*((datetime.strptime(off_on_df.iloc[i]["RDL"], '%Y-%m-%d') -
datetime.strptime(from_date, '%Y-%m-%d')).days)/360)) / 2,
f_acf=0.5, error=False,
p=off_on_df.iloc[i]["Price on 2020-07-31"])['Opt. YTM']
for i in range(len(off_on_df))]
# Add the Years Left to Maturity
off_on_df["Years Left to Maturity"] = [
(round(2*((datetime.strptime(off_on_df.iloc[i]["RDL"], '%Y-%m-%d') -
datetime.strptime(from_date, '%Y-%m-%d')).days)/360)) / 2
for i in range(len(off_on_df))]
off_on_df.sort_values('RDL', inplace=True)
display(off_on_df)
off_on_df["YTM implied by 2020-07-31 Price"].iplot(
title="Yield To Maturity of US Treasury Bonds with different issue dates fixed and different Coupon rates")
| DSCD | NAME | ID | TERM | RV | C | CTYP | RDL | Price at issue | CD | CF | YTM | Price on 2020-07-31 | YTM implied by 2020-07-31 Price | Years Left to Maturity | |
| 29/12/2020 | 613V2R | UTD.STS OF AMERICA 2020 ZERO 29/12/20 | 28/07/2020 | 0.5 | 100 | 0 | ZERO | 29/12/2020 | 99.9469 | [2021-02-01 00:00:00] | [0.0] | 0.001063 | 99.9559 | 0.000882 | 0.5 |
| 31/07/2021 | 235FFA | US TREASURY NOTE 2019 1 3/4% 31/07/21 BD-2021 | 31/07/2019 | 2 | 100 | 1.75 | FIX | 31/07/2021 | 99.793 | [2020-01-31 00:00:00, 2020-07-31 00:00:00, 202... | [1.75, 1.75, 1.75, 1.75] | 0.018559 | 101.6094 | 0.001389 | 1 |
| 31/12/2021 | 247DK9 | US TREASURY NOTE 2019 1 5/8% 31/12/21 BL-2021 | 31/12/2019 | 2 | 100 | 1.625 | FIX | 31/12/2021 | 100.0742 | [2020-06-30 00:00:00, 2020-12-31 00:00:00, 202... | [1.625, 1.625, 1.625, 1.625] | 0.015872 | 102.1016 | 0.002208 | 1.5 |
| 31/07/2022 | 613XGW | US TREASURY NOTE 2020 1/8% 31/07/22 BD-2022 | 31/07/2020 | 2 | 100 | 0.125 | FIX | 31/07/2022 | 100.0313 | [2021-02-01 00:00:00, 2021-08-02 00:00:00, 202... | [0.125, 0.125, 0.125, 0.125] | 0.001093 | 100.0313 | 0.001093 | 2 |
| 31/12/2022 | 823D0N | US TREASURY NOTE 2015 2 1/8% 31/12/22 T-2022 | 31/12/2015 | 7 | 100 | 2.125 | FIX | 31/12/2022 | 100.2031 | [2016-06-30 00:00:00, 2017-01-03 00:00:00, 201... | [2.125, 2.125, 2.125, 2.125, 2.125, 2.125, 2.1... | 0.020937 | 104.8281 | 0.001883 | 2.5 |
| 31/07/2023 | 210EV1 | US TREASURY NOTE 2018 2 3/4% 31/07/23 AB-2023 | 31/07/2018 | 5 | 100 | 2.75 | FIX | 31/07/2023 | 99.5469 | [2019-01-31 00:00:00, 2019-07-31 00:00:00, 202... | [2.75, 2.75, 2.75, 2.75, 2.75, 2.75, 2.75, 2.7... | 0.028479 | 107.8438 | 0.001295 | 3 |
| 31/12/2023 | 218QH0 | US TREASURY NOTE 2018 2 5/8% 31/12/23 AG-2023 | 31/12/2018 | 5 | 100 | 2.625 | FIX | 31/12/2023 | 100.5391 | [2019-07-01 00:00:00, 2019-12-31 00:00:00, 202... | [2.625, 2.625, 2.625, 2.625, 2.625, 2.625, 2.6... | 0.025096 | 108.4609 | 0.00198 | 3.5 |
| 31/07/2024 | 235FFD | US TREASURY NOTE 2019 1 3/4% 31/07/24 AB-2024 | 31/07/2019 | 5 | 100 | 1.75 | FIX | 31/07/2024 | 99.6563 | [2020-01-31 00:00:00, 2020-07-31 00:00:00, 202... | [1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.7... | 0.018222 | 106.3203 | 0.001641 | 4 |
| 31/12/2024 | 247DLH | US TREASURY NOTE 2019 1 3/4% 31/12/24 AH-2024 | 31/12/2019 | 5 | 100 | 1.75 | FIX | 31/12/2024 | 100.2734 | [2020-06-30 00:00:00, 2020-12-31 00:00:00, 202... | [1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.7... | 0.016927 | 106.8828 | 0.002124 | 4.5 |
| 31/07/2025 | 613XGU | US TREASURY NOTE 2020 1/4% 31/07/25 AB-2025 | 31/07/2020 | 5 | 100 | 0.25 | FIX | 31/07/2025 | 100.2031 | [2021-02-01 00:00:00, 2021-08-02 00:00:00, 202... | [0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.2... | 0.002091 | 100.2031 | 0.002091 | 5 |
| 31/12/2025 | 218QJQ | US TREASURY NOTE 2018 2 5/8% 31/12/25 T-2025 | 31/12/2018 | 7 | 100 | 2.625 | FIX | 31/12/2025 | 100.25 | [2019-07-01 00:00:00, 2019-12-31 00:00:00, 202... | [2.625, 2.625, 2.625, 2.625, 2.625, 2.625, 2.6... | 0.025857 | 112.7344 | 0.002895 | 5.5 |
| 31/07/2026 | 235FF9 | US TREASURY NOTE 2019 1 7/8% 31/07/26 N-2026 | 31/07/2019 | 7 | 100 | 1.875 | FIX | 31/07/2026 | 99.7813 | [2020-01-31 00:00:00, 2020-07-31 00:00:00, 202... | [1.875, 1.875, 1.875, 1.875, 1.875, 1.875, 1.8... | 0.019085 | 109.2891 | 0.003111 | 6 |
| 31/12/2026 | 247DLR | US TREASURY NOTE 2019 1 3/4% 31/12/26 T-2026 | 31/12/2019 | 7 | 100 | 1.75 | FIX | 31/12/2026 | 99.4375 | [2020-06-30 00:00:00, 2020-12-31 00:00:00, 202... | [1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.7... | 0.01836 | 108.8984 | 0.003635 | 6.5 |
| 31/07/2027 | 613XG1 | US TREASURY NOTE 2020 3/8% 31/07/27 N-2027 | 31/07/2020 | 7 | 100 | 0.375 | FIX | 31/07/2027 | 99.914 | [2021-02-01 00:00:00, 2021-08-02 00:00:00, 202... | [0.375, 0.375, 0.375, 0.375, 0.375, 0.375, 0.3... | 0.003875 | 99.914 | 0.003875 | 7 |
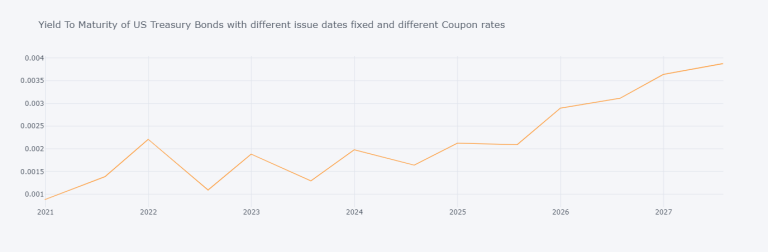
This vertical zigzagging is an unexpected pattern. The reason for which it is unexpected is that an economic agent ought to be able to exploit arbitrage opportunities brought up by such price discrepancies with other securities (*e.g.*: Swaps).
The only Zero Coupon Bond in our off_on_df data-frame is the 1st one (the 0th one in 'Python language'); we can use it as a 1st value from which to compute/Bootstrap all other Zero-Coupon-Equivalent Bond Spot-Rates:
off_on_df.iloc[0]["YTM implied by 2020-07-31 Price"]
0.0008823891336079769
spot_rates = [0.0008823891336079769] # This number is from the YTM of the only ZCB we've got as per the above.
for i in range(len(spot_rates), len(off_on_df)):
spot_rates.append(Spot_Rate_Last(
fv=off_on_df.iloc[i]["RV"], sr=spot_rates, f=0.5,
m=off_on_df.iloc[i]["Years Left to Maturity"],
c=off_on_df.iloc[i]["RV"] * off_on_df.iloc[i]["C"] / 100,
p=off_on_df.iloc[i]["Price on 2020-07-31"]))
off_on_df["Spot Rates as of 2020-07-31"] = spot_rates
off_on_df["YTM"][0]
0.0010625642216017055
off_on_df
| DSCD | NAME | ID | TERM | RV | C | CTYP | RDL | Price at issue | CD | CF | YTM | Price on 2020-07-31 | YTM implied by 2020-07-31 Price | Years Left to Maturity | Spot Rates as of 2020-07-31 | |
| 29/12/2020 | 613V2R | UTD.STS OF AMERICA 2020 ZERO 29/12/20 | 28/07/2020 | 0.5 | 100 | 0 | ZERO | 29/12/2020 | 99.9469 | [2021-02-01 00:00:00] | [0.0] | 0.001063 | 99.9559 | 0.000882 | 0.5 | 0.000882 |
| 31/07/2021 | 235FFA | US TREASURY NOTE 2019 1 3/4% 31/07/21 BD-2021 | 31/07/2019 | 2 | 100 | 1.75 | FIX | 31/07/2021 | 99.793 | [2020-01-31 00:00:00, 2020-07-31 00:00:00, 202... | [1.75, 1.75, 1.75, 1.75] | 0.018559 | 101.6094 | 0.001389 | 1 | 0.001391 |
| 31/12/2021 | 247DK9 | US TREASURY NOTE 2019 1 5/8% 31/12/21 BL-2021 | 31/12/2019 | 2 | 100 | 1.625 | FIX | 31/12/2021 | 100.0742 | [2020-06-30 00:00:00, 2020-12-31 00:00:00, 202... | [1.625, 1.625, 1.625, 1.625] | 0.015872 | 102.1016 | 0.002208 | 1.5 | 0.002216 |
| 31/07/2022 | 613XGW | US TREASURY NOTE 2020 1/8% 31/07/22 BD-2022 | 31/07/2020 | 2 | 100 | 0.125 | FIX | 31/07/2022 | 100.0313 | [2021-02-01 00:00:00, 2021-08-02 00:00:00, 202... | [0.125, 0.125, 0.125, 0.125] | 0.001093 | 100.0313 | 0.001093 | 2 | 0.001093 |
| 31/12/2022 | 823D0N | US TREASURY NOTE 2015 2 1/8% 31/12/22 T-2022 | 31/12/2015 | 7 | 100 | 2.125 | FIX | 31/12/2022 | 100.2031 | [2016-06-30 00:00:00, 2017-01-03 00:00:00, 201... | [2.125, 2.125, 2.125, 2.125, 2.125, 2.125, 2.1... | 0.020937 | 104.8281 | 0.001883 | 2.5 | 0.001892 |
| 31/07/2023 | 210EV1 | US TREASURY NOTE 2018 2 3/4% 31/07/23 AB-2023 | 31/07/2018 | 5 | 100 | 2.75 | FIX | 31/07/2023 | 99.5469 | [2019-01-31 00:00:00, 2019-07-31 00:00:00, 202... | [2.75, 2.75, 2.75, 2.75, 2.75, 2.75, 2.75, 2.7... | 0.028479 | 107.8438 | 0.001295 | 3 | 0.001284 |
| 31/12/2023 | 218QH0 | US TREASURY NOTE 2018 2 5/8% 31/12/23 AG-2023 | 31/12/2018 | 5 | 100 | 2.625 | FIX | 31/12/2023 | 100.5391 | [2019-07-01 00:00:00, 2019-12-31 00:00:00, 202... | [2.625, 2.625, 2.625, 2.625, 2.625, 2.625, 2.6... | 0.025096 | 108.4609 | 0.00198 | 3.5 | 0.001998 |
| 31/07/2024 | 235FFD | US TREASURY NOTE 2019 1 3/4% 31/07/24 AB-2024 | 31/07/2019 | 5 | 100 | 1.75 | FIX | 31/07/2024 | 99.6563 | [2020-01-31 00:00:00, 2020-07-31 00:00:00, 202... | [1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.7... | 0.018222 | 106.3203 | 0.001641 | 4 | 0.001641 |
| 31/12/2024 | 247DLH | US TREASURY NOTE 2019 1 3/4% 31/12/24 AH-2024 | 31/12/2019 | 5 | 100 | 1.75 | FIX | 31/12/2024 | 100.2734 | [2020-06-30 00:00:00, 2020-12-31 00:00:00, 202... | [1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.7... | 0.016927 | 106.8828 | 0.002124 | 4.5 | 0.002141 |
| 31/07/2025 | 613XGU | US TREASURY NOTE 2020 1/4% 31/07/25 AB-2025 | 31/07/2020 | 5 | 100 | 0.25 | FIX | 31/07/2025 | 100.2031 | [2021-02-01 00:00:00, 2021-08-02 00:00:00, 202... | [0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.2... | 0.002091 | 100.2031 | 0.002091 | 5 | 0.002093 |
| 31/12/2025 | 218QJQ | US TREASURY NOTE 2018 2 5/8% 31/12/25 T-2025 | 31/12/2018 | 7 | 100 | 2.625 | FIX | 31/12/2025 | 100.25 | [2019-07-01 00:00:00, 2019-12-31 00:00:00, 202... | [2.625, 2.625, 2.625, 2.625, 2.625, 2.625, 2.6... | 0.025857 | 112.7344 | 0.002895 | 5.5 | 0.002966 |
| 31/07/2026 | 235FF9 | US TREASURY NOTE 2019 1 7/8% 31/07/26 N-2026 | 31/07/2019 | 7 | 100 | 1.875 | FIX | 31/07/2026 | 99.7813 | [2020-01-31 00:00:00, 2020-07-31 00:00:00, 202... | [1.875, 1.875, 1.875, 1.875, 1.875, 1.875, 1.8... | 0.019085 | 109.2891 | 0.003111 | 6 | 0.003169 |
| 31/12/2026 | 247DLR | US TREASURY NOTE 2019 1 3/4% 31/12/26 T-2026 | 31/12/2019 | 7 | 100 | 1.75 | FIX | 31/12/2026 | 99.4375 | [2020-06-30 00:00:00, 2020-12-31 00:00:00, 202... | [1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.75, 1.7... | 0.01836 | 108.8984 | 0.003635 | 6.5 | 0.003712 |
| 31/07/2027 | 613XG1 | US TREASURY NOTE 2020 3/8% 31/07/27 N-2027 | 31/07/2020 | 7 | 100 | 0.375 | FIX | 31/07/2027 | 99.914 | [2021-02-01 00:00:00, 2021-08-02 00:00:00, 202... | [0.375, 0.375, 0.375, 0.375, 0.375, 0.375, 0.3... | 0.003875 | 99.914 | 0.003875 | 7 | 0.003893 |
off_on_df[["YTM implied by 2020-07-31 Price", "Spot Rates as of 2020-07-31"]].iplot(
title="On- and Off-the-run US Treasury Bonds with Zero or Fixed (and different) Coupon Rates")
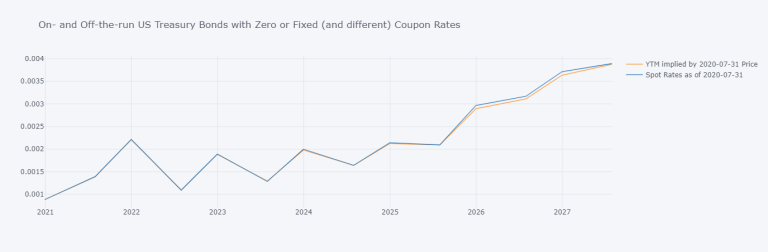
Let's make a function for it, call it Get_dsws_spot_rates_from_df when working from a known data-frame, and Get_dsws_spot_rates otherwise:
instruments = ["628GA1", "628GAL", "628GD0", "628GF5", "628GDZ", "610JPM", '208PR9', "218QH0", "233HJH", "247DLH", "610JRN", "233HJK", "247DLR", "610JR7"]
fields = ["DSCD", "NAME", "ID", "TERM", "RV", "C", "CTYP", "RDL"]
_df = pandas.DataFrame()
for i in instruments:
__df = ds.get_data(tickers=i, kind=0, fields=fields)
_df = _df.append(pandas.DataFrame(
data=list(__df['Value'].values), index=fields).T)
_df
| DSCD | NAME | ID | TERM | RV | C | CTYP | RDL | |
| 0 | 628GA1 | UTD.STS OF AMERICA 2020 ZERO 01/07/21 | 31/12/2020 | 0.5 | 100 | 0 | ZERO | 01/07/2021 |
| 0 | 628GAL | UTD.STS OF AMERICA 2020 ZERO 30/12/21 | 31/12/2020 | 1 | 100 | 0 | ZERO | 30/12/2021 |
| 0 | 628GD0 | US TREASURY NOTE 2020 1/8% 31/12/22 BL-2022 | 31/12/2020 | 2 | 100 | 0.125 | FIX | 31/12/2022 |
| 0 | 628GF5 | US TREASURY NOTE 2020 3/8% 31/12/25 AH-2025 | 31/12/2020 | 5 | 100 | 0.375 | FIX | 31/12/2025 |
| 0 | 628GDZ | US TREASURY NOTE 2020 5/8% 31/12/27 T-2027 | 31/12/2020 | 7 | 100 | 0.625 | FIX | 31/12/2027 |
| 0 | 610JPM | US TREASURY NOTE 2020 1/8% 30/06/22 BC-2022 | 30/06/2020 | 2 | 100 | 0.125 | FIX | 30/06/2022 |
| 0 | 208PR9 | US TREASURY NOTE 2018 2 5/8% 30/06/23 AA-2023 | 30/06/2018 | 5 | 100 | 2.625 | FIX | 30/06/2023 |
| 0 | 218QH0 | US TREASURY NOTE 2018 2 5/8% 31/12/23 AG-2023 | 31/12/2018 | 5 | 100 | 2.625 | FIX | 31/12/2023 |
| 0 | 233HJH | US TREASURY NOTE 2019 1 3/4% 30/06/24 AA-2024 | 30/06/2019 | 5 | 100 | 1.75 | FIX | 30/06/2024 |
| 0 | 247DLH | US TREASURY NOTE 2019 1 3/4% 31/12/24 AH-2024 | 31/12/2019 | 5 | 100 | 1.75 | FIX | 31/12/2024 |
| 0 | 610JRN | US TREASURY NOTE 2020 1/4% 30/06/25 AA-2025 | 30/06/2020 | 5 | 100 | 0.25 | FIX | 30/06/2025 |
| 0 | 233HJK | US TREASURY NOTE 2019 1 7/8% 30/06/26 M-2026 | 30/06/2019 | 7 | 100 | 1.875 | FIX | 30/06/2026 |
| 0 | 247DLR | US TREASURY NOTE 2019 1 3/4% 31/12/26 T-2026 | 31/12/2019 | 7 | 100 | 1.75 | FIX | 31/12/2026 |
| 0 | 610JR7 | US TREASURY NOTE 2020 1/2% 30/06/27 M-2027 | 30/06/2020 | 7 | 100 | 0.5 | FIX | 30/06/2027 |
on_off_df_as_of_2020_12_31 = Get_dsws_spot_rates(
point_in_time="2020-12-31", coupon_paying_freq=0.5,
instruments=instruments)
on_off_df_as_of_2020_12_31
| DSCD | NAME | ID | TERM | RV | C | CTYP | RDL | Price on 2020-12-31 | YTM implied by 2020-12-31 Price | Years from 2020-12-31 to Maturity | Spot Rates as of 2020-12-31 | |
| RD | ||||||||||||
| 01/07/2021 | 628GA1 | UTD.STS OF AMERICA 2020 ZERO 01/07/21 | 31/12/2020 | 0.5 | 100 | 0 | ZERO | 01/07/2021 | 99.9555 | 0.00089 | 0.5 | 0.00089 |
| 30/12/2021 | 628GAL | UTD.STS OF AMERICA 2020 ZERO 30/12/21 | 31/12/2020 | 1 | 100 | 0 | ZERO | 30/12/2021 | 99.89 | 0.001101 | 1 | 0.001101 |
| 30/06/2022 | 610JPM | US TREASURY NOTE 2020 1/8% 30/06/22 BC-2022 | 30/06/2020 | 2 | 100 | 0.125 | FIX | 30/06/2022 | 100.0156 | 0.001146 | 1.5 | 0.001146 |
| 31/12/2022 | 628GD0 | US TREASURY NOTE 2020 1/8% 31/12/22 BL-2022 | 31/12/2020 | 2 | 100 | 0.125 | FIX | 31/12/2022 | 100 | 0.00125 | 2 | 0.00125 |
| 30/06/2023 | 208PR9 | US TREASURY NOTE 2018 2 5/8% 30/06/23 AA-2023 | 30/06/2018 | 5 | 100 | 2.625 | FIX | 30/06/2023 | 106.1563 | 0.001567 | 2.5 | 0.001578 |
| 31/12/2023 | 218QH0 | US TREASURY NOTE 2018 2 5/8% 31/12/23 AG-2023 | 31/12/2018 | 5 | 100 | 2.625 | FIX | 31/12/2023 | 107.3203 | 0.001773 | 3 | 0.001789 |
| 30/06/2024 | 233HJH | US TREASURY NOTE 2019 1 3/4% 30/06/24 AA-2024 | 30/06/2019 | 5 | 100 | 1.75 | FIX | 30/06/2024 | 105.3516 | 0.002144 | 3.5 | 0.002163 |
| 31/12/2024 | 247DLH | US TREASURY NOTE 2019 1 3/4% 31/12/24 AH-2024 | 31/12/2019 | 5 | 100 | 1.75 | FIX | 31/12/2024 | 105.9141 | 0.002627 | 4 | 0.002658 |
| 30/06/2025 | 610JRN | US TREASURY NOTE 2020 1/4% 30/06/25 AA-2025 | 30/06/2020 | 5 | 100 | 0.25 | FIX | 30/06/2025 | 99.7265 | 0.003113 | 4.5 | 0.003119 |
| 31/12/2025 | 628GF5 | US TREASURY NOTE 2020 3/8% 31/12/25 AH-2025 | 31/12/2020 | 5 | 100 | 0.375 | FIX | 31/12/2025 | 100.0703 | 0.003608 | 5 | 0.003621 |
| 30/06/2026 | 233HJK | US TREASURY NOTE 2019 1 7/8% 30/06/26 M-2026 | 30/06/2019 | 7 | 100 | 1.875 | FIX | 30/06/2026 | 107.875 | 0.004249 | 5.5 | 0.004337 |
| 31/12/2026 | 247DLR | US TREASURY NOTE 2019 1 3/4% 31/12/26 T-2026 | 31/12/2019 | 7 | 100 | 1.75 | FIX | 31/12/2026 | 107.4141 | 0.004944 | 6 | 0.005053 |
| 30/06/2027 | 610JR7 | US TREASURY NOTE 2020 1/2% 30/06/27 M-2027 | 30/06/2020 | 7 | 100 | 0.5 | FIX | 30/06/2027 | 99.5313 | 0.005736 | 6.5 | 0.005777 |
| 31/12/2027 | 628GDZ | US TREASURY NOTE 2020 5/8% 31/12/27 T-2027 | 31/12/2020 | 7 | 100 | 0.625 | FIX | 31/12/2027 | 99.8438 | 0.006479 | 7 | 0.006542 |
on_off_df_as_of_2020_12_31[
["YTM implied by 2020-12-31 Price", "Spot Rates as of 2020-12-31"]].iplot(
title="On- and Off-the-run US Treasury Bonds with Zero or Fixed (and different) Coupon Rates")
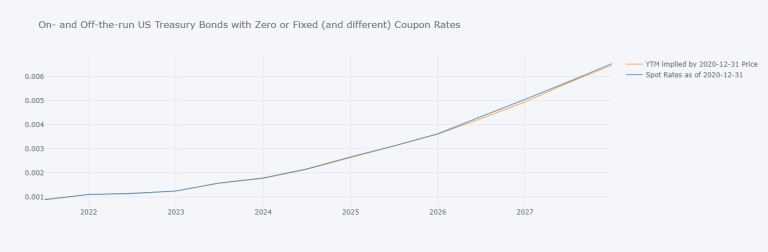
Accrued Interests
Lastly - when it comes to Yields - if one was to buy a Bond in the secondary market at a time other than just after a Coupon was paid, the Bond's seller would loose out on the upcoming Coupon payment. In other words, if a Bond (issued years ago with \$100 Face Value) was to pay a \$0.1 Coupon a day, and was sold on the 30th of Jan., the Bond's seller would have gathered (\$0.1 * days in a year * 0.5 = \$0.1 * 360 * 0.5 =) \$18.6 in Coupon payments that half-year (in the 6 previous months); however, if the Coupon is only paid every 6 months on the 31st of Jan. and 31st of Jul., the Bond's seller would have gathered no Coupon payments that half-year. To compensate for this lost payment, Bond sellers on the secondary market do not tend to sell at the NPV, i.e.: they tend not to Bid at a Clean Price. (The clean price is the NPV in the 'lingo'.) Instead, they tend to Bid at a Dirty Price that incorporates this 'Coupon payment loss' in an arithmetic/straight-line method; this 'loss' is called the Accrued, think of it as accrued interest that the seller would have had and insists on via this Dirty Price premium. One can see - thanks to the aforementioned relationship between a Bond's price and Yield - that if the price differs, so does its YTM. This - evidently - does not apply to Zero-Coupon-Bonds (ZCB); or rather: ZCB's Clean and Dirty Prices are the same. Let's add Clean and Dirty classifications:
Let's say that our investor considers only the bonds in our on_off_df_as_of_2020_12_31 data-frame, but on 2021-03-31, then we can accrue coupons:
on_off_df_as_of_2020_12_31 = Get_dsws_spot_rates(
point_in_time="2020-12-31", coupon_paying_freq=0.5,
instruments=instruments, dirty=True)
on_off_df_as_of_2020_12_31
If you are interested in compounding, straight-line / arithmetic / geometric, accruals please read Part 1 on risk-free rates. Risk free rates can be computed with the bellow from Zero-Coupon-Bonds. We can therefore now use Coupon-Paying-Bonds' Spot Rates to calculate risk free rates with the below:
Where $d$ is the compounding frequency
It is this simple because YTMs are annualised - and thus are Spot-Rates. E.g.: If ${SR}_{\text{SYTN}_{"2020-12-31"}, 2020-12-31} \approx 0.006541635089218456$ : $$r_f \approx \sqrt[365]{1 + 0.006541635089218456} - 1 \approx 0.000017864081344409755 \approx 0.00179 \%$$ since:
((1 + on_off_df_as_of_2020_12_31.iloc[-1, -1])**(1/365)) - 1
1.7864081344409755e-05
This is the YTM implied daily risk-free rate ($r_f$) of our bond. A similar 'weekly' - 7 day - or 'monthly' - 30 day - rate can be made by letting $d$ be the number of weeks or months for the year in question.
Why would one use 30 days (as per our example)? Because the 1-, 2-, and 3-month rates are equivalent to the 30-, 60-, and 90-day dates respectively, reported on the Board's Commercial Paper Web page. This is as per reference (see more here) with that said, one ought to use the exact number of days to maturity.
Using the defined function ZCB_YTM_Implied_r_f from Part 1 we can easily compute risk free rates as per the Python code r_f = ((ytm + 1)**(1/d))-1 for $r_f$ values of a frequency $f_{acf}$ which we've set to 6-months such that:
on_off_df_as_of_2020_12_31["rf"] = list(
((on_off_df_as_of_2020_12_31["Spot Rates as of 2020-12-31"] + 1)**(1/4))-1)
on_off_df_as_of_2020_12_31
| DSCD | NAME | ID | TERM | RV | C | CTYP | RDL | Price on 2020-12-31 | YTM implied by 2020-12-31 Price | Dirty Price on 2020-12-31 | Years from 2020-12-31 to Maturity | Dirty Years from 2020-12-31 to Maturity | Spot Rates as of 2020-12-31 | rf | |
| RD | |||||||||||||||
| 01/07/2021 | 628GA1 | UTD.STS OF AMERICA 2020 ZERO 01/07/21 | 31/12/2020 | 0.5 | 100 | 0 | ZERO | 01/07/2021 | 99.9555 | 0.00089 | 99.9555 | 0.5 | 0.505556 | 0.00089 | 0.000223 |
| 30/12/2021 | 628GAL | UTD.STS OF AMERICA 2020 ZERO 30/12/21 | 31/12/2020 | 1 | 100 | 0 | ZERO | 30/12/2021 | 99.89 | 0.001101 | 99.89 | 1 | 1.011111 | 0.001101 | 0.000275 |
| 30/06/2022 | 610JPM | US TREASURY NOTE 2020 1/8% 30/06/22 BC-2022 | 30/06/2020 | 2 | 100 | 0.125 | FIX | 30/06/2022 | 100.0156 | 0.001146 | 100.076017 | 1.5 | 1.516667 | 0.001146 | 0.000286 |
| 31/12/2022 | 628GD0 | US TREASURY NOTE 2020 1/8% 31/12/22 BL-2022 | 31/12/2020 | 2 | 100 | 0.125 | FIX | 31/12/2022 | 100 | 0.00125 | 100.121528 | 2 | 2.027778 | 0.00125 | 0.000312 |
| 30/06/2023 | 208PR9 | US TREASURY NOTE 2018 2 5/8% 30/06/23 AA-2023 | 30/06/2018 | 5 | 100 | 2.625 | FIX | 30/06/2023 | 106.1563 | 0.001567 | 107.388592 | 2.5 | 2.530556 | 0.001578 | 0.000394 |
| 31/12/2023 | 218QH0 | US TREASURY NOTE 2018 2 5/8% 31/12/23 AG-2023 | 31/12/2018 | 5 | 100 | 2.625 | FIX | 31/12/2023 | 107.3203 | 0.001773 | 109.835925 | 3 | 3.041667 | 0.001789 | 0.000447 |
| 30/06/2024 | 233HJH | US TREASURY NOTE 2019 1 3/4% 30/06/24 AA-2024 | 30/06/2019 | 5 | 100 | 1.75 | FIX | 30/06/2024 | 105.3516 | 0.002144 | 106.143961 | 3.5 | 3.547222 | 0.002163 | 0.00054 |
| 31/12/2024 | 247DLH | US TREASURY NOTE 2019 1 3/4% 31/12/24 AH-2024 | 31/12/2019 | 5 | 100 | 1.75 | FIX | 31/12/2024 | 105.9141 | 0.002627 | 107.562017 | 4 | 4.058333 | 0.002658 | 0.000664 |
| 30/06/2025 | 610JRN | US TREASURY NOTE 2020 1/4% 30/06/25 AA-2025 | 30/06/2020 | 5 | 100 | 0.25 | FIX | 30/06/2025 | 99.7265 | 0.003113 | 99.836222 | 4.5 | 4.561111 | 0.003119 | 0.000779 |
| 31/12/2025 | 628GF5 | US TREASURY NOTE 2020 3/8% 31/12/25 AH-2025 | 31/12/2020 | 5 | 100 | 0.375 | FIX | 31/12/2025 | 100.0703 | 0.003608 | 100.418217 | 5 | 5.072222 | 0.003621 | 0.000904 |
| 30/06/2026 | 233HJK | US TREASURY NOTE 2019 1 7/8% 30/06/26 M-2026 | 30/06/2019 | 7 | 100 | 1.875 | FIX | 30/06/2026 | 107.875 | 0.004249 | 108.671875 | 5.5 | 5.575 | 0.004337 | 0.001082 |
| 31/12/2026 | 247DLR | US TREASURY NOTE 2019 1 3/4% 31/12/26 T-2026 | 31/12/2019 | 7 | 100 | 1.75 | FIX | 31/12/2026 | 107.4141 | 0.004944 | 109.013406 | 6 | 6.086111 | 0.005053 | 0.001261 |
| 30/06/2027 | 610JR7 | US TREASURY NOTE 2020 1/2% 30/06/27 M-2027 | 30/06/2020 | 7 | 100 | 0.5 | FIX | 30/06/2027 | 99.5313 | 0.005736 | 99.736856 | 6.5 | 6.588889 | 0.005777 | 0.001441 |
| 31/12/2027 | 628GDZ | US TREASURY NOTE 2020 5/8% 31/12/27 T-2027 | 31/12/2020 | 7 | 100 | 0.625 | FIX | 31/12/2027 | 99.8438 | 0.006479 | 100.4063 | 7 | 7.1 | 0.006542 | 0.001631 |
Excess Returns from Spot Rates of Coupon-Paying-Bonds
Now that we have risk-free rates, it is easy to compute the excess return of any instrument.
The excess returns ($XSR_{t}$) at time t are computed from its price ($P_{t}$) and the chosen risk free rate (${r_f}_t$) such that:
$$\begin{equation} XSR_{t} = \frac{P_{t} - P_{t-1}}{P_{t-1}} - {r_f}_t \end{equation}$$Example: The S&P500 index: With the 7 Year Treasury Note issued on 2020-12-31:
P_SPX = ds.get_data(tickers='S&PCOMP',
fields="X",
start='2020-12-30',
end='2020-12-31',
freq='D')
r_f = ((on_off_df_as_of_2020_12_31.iloc[-1, -1] + 1)**(1/365))-1 # Remember that ' on_off_df_as_of_2020_12_31.iloc[-1, -1] ' is our Spot Rate
XSR_SPX = ((P_SPX.iloc[-1, -1] - P_SPX.iloc[0, -1])/P_SPX.iloc[0, -1]) - r_f
XSR_SPX
0.006434371749798833
We can see that using published rates by sovereign institutions such as the US Treasury is simple, as seen in the Zero Coupon Bond article. However, when we include Coupon Paying Bonds and secondary markets - as traders tend to - it gets rather complicated. That is where Python and the functions described above (discoverable in the source code on GitHub) are useful to (i) understand the underlying mechanism of Fixed Income Markets and(ii) use concepts such as Yields and Spot Rates.
References
Datastream
Yield Optimisation
Miscellaneous
- What Is Accrued Interest, and Why Do I Have to Pay It When I Buy a Bond?
- straight-line amortization of Coupons
- Calculating U.S. Treasury Pricing
- Bootstrapped spot rates with missing bonds
- Bootstrapping the Zero Curve and Forward Rates - Straight Line Interpolation
- Cubic Spline Interpolation
- Building Search into your Application Workflow
- What is Bootstrapping?
- How to calculate Yield To Maturity with Python
- Number of days between 2 dates, excluding weekends